You may also like

problem icon

Polydron

This activity investigates how you might make squares and pentominoes from Polydron.

problem icon

A Cartesian Puzzle

Find the missing coordinates which will form these eight quadrilaterals. These coordinates themselves will then form a shape with rotational and line symmetry.

problem icon

Symmetry Challenge

Systematically explore the range of symmetric designs that can be created by shading parts of the motif below. Use normal square lattice paper to record your results.

Coordinate Challenge

Stage: 2 Challenge Level: Challenge Level:1

We had lots of solutions to this problem but not many of you told us how you got your solutions. Luis and Freddie, who go to Newton Prep, sent in well-explained solutions. Here is what Luis wrote:



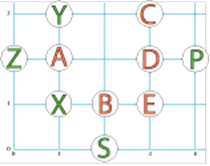
The first thing I worked out is that the letter at (4,2) is not symmetrical in any way, the only letter that isn't symmetrical in any way is the letter P.
Then I worked out that at (0,2) and (1,2) are the ends of the alphabet and had to be A and Z but I needed to know which one went where so I looked at the clues. One said that (0,2) and (2,0) have rotational symmetry which means that A is on (1,2) and Z is on (0,2).
Then I saw the clue that said that (3,3), (3,2) and (3,1) are all consecutive in the alphabet, because the A and the Z are already used, it has to be C, D and E because it says that (3,3) is made of only curved lines.
Then I saw that one of the clues said that (2,0) is only made of curved lines, so (2,0) is the S.
(4,2) is not symmetrical in any way so (4,2) is a P.
The first clue says that (1,1) and (1,3) have a vertical line of symmetry, another clue says that (1,1) also has a vertical line of symmetry, which means that (1,1) is a X and (1,3) is a Y, which leaves the B which is at (2,1) because a clue says that at (2,1) there is a letter with a horizontal line of symmetry.

Many children from Stradbroke Primary School sent an image of their solution. Here is George's:

solution

Well done!


The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.