Well it all started by drawing some equilateral triangles so that they made a regular hexagon:



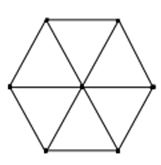
Then we made a bigger one:




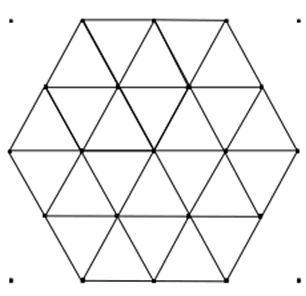
Well there was the thought about how many dots there were in various places.
On the circumference there were 6 and then 12 on the second one.
But what about the number inside? And, how do you count them?
Well we counted 1 in the first and 7 in the second one.

We'll leave you to try the third size and count the dots.

Then there are the lines.
We counted just the number of straight lines ignoring their lengths.
There were 12 in the first and 15 for the second. How many for the next we wondered?

If you remember this all started with a hexagon made out of six equilateral triangles.
So we wondered how many lines of unit length the same as the side of one of those triangles there are? Well we counted 12 on the first and 42 in the 2nd one. So what about the 3rd one?

There are lots of paths for you to investigate here. Let us know what patterns you discover and any explanations that you work out.



Then there was the idea of what if the equilateral triangles had longer sides?
The first would look like this:



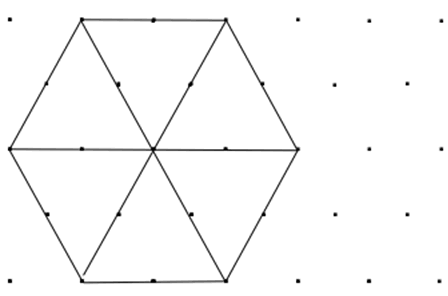
And the second:



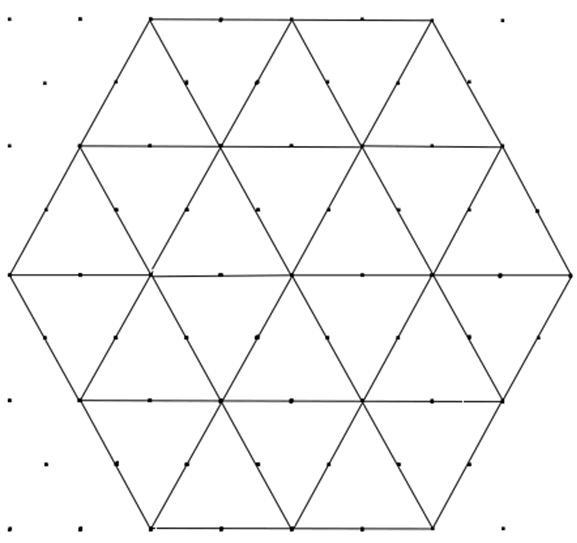
So again we thought about how many dots there were in various places.
On the circumference there were 12 and then 24 on the bigger one.
But what about the number inside? And, how do you count them?
Well we counted 7 dots inside the first.
The second one was a bit harder and we tried it different ways and finally agreed on 37.
So the total number of dots for the first one is 19. And the number of dots for the bigger one is 24+37=61.

We have not noticed those numbers before coming up in a number pattern, so we need the next bigger hexagon with the lengths of three triangles on each of the six edges. I'm not going to draw that one but you might like to ...

Then there are the lines.
We counted just the number of straight lines, ignoring their lengths.
There were 9 for the first hexagon and 15 for the bigger one.
How many for the third?

If you remember this all started with a hexagon made out of six equilateral triangles.
So we wondered how many lines of length the same as the side of one of those triangles there are?
We counted 12 in the first one and 42 in the second one.
It looked as if there was going to be a large number for the third largest hexagon.

Using triangles of course made it obvious to count how many we used. 6 for the first, 24 for the second, how many for the third one?

Again, you can investigate the dots, lines and triangles for this larger size too.
What do you find?
Can you explain the patterns?