 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Square Areas



- Problem
- Getting Started
- Student Solutions
 |
 |
The area of the inner square has area of 0.2 square units. First draw the original square, then remove the triangles. The triangles can then be added to the trapeziums to make four equal squares. This gives a total of five equal squares which have a total area of 1 square unit. Therefore each of the smaller squares must have an area of 0.2 square units.
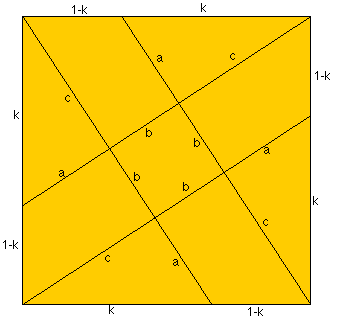
If we don't use the midpoints on the sides of the big square the problem can be generalised by considering the lengths as shown in the diagram. In the above solution k = 1/2 and a = b .
By enlargement (or similar triangles) c = ka
.
Using Pythagoras Theorem twice we get $a^2 + c^2 = k^2$ and also
$(a + b + c)^2 = 1 + k^2$
By some routine algebra we get $a^2 = k^2/(1 + k^2)$ and the area of the inner square is $b^2 = (1 - k)^2/(1 + k^2).$