Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Square Ratio
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: 1:3
Using lengths

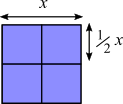
If the areas are in the ratio $1:4,$ then the sides are in the ratio $1:2$


$x=s+l,$ and
$\frac12 x+s+s = x\\
\Rightarrow x + 4s = 2x\\
\Rightarrow x = 4s$
So $4s = s + l \Rightarrow 3s = l$ so the ratio is $1:3$.
Using areas
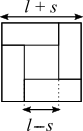
$(l-s)^2 : (l+s)^2 = 1:4$
$\Rightarrow(l-s)^2\times4 = (l+s)^2$
$\Rightarrow4 = \dfrac{(l+s)^2}{(l-s)^2}$
$\Rightarrow2 = \dfrac{l+s}{l-s}$
$\Rightarrow 2l-2s = l+s$
$\Rightarrow l = 3s$
So the ratio is $1:3$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Sixational
The nth term of a sequence is given by the formula n^3 + 11n. Find the first four terms of the sequence given by this formula and the first term of the sequence which is bigger than one million. Prove that all terms of the sequence are divisible by 6.