Doesn't Add Up printable sheet

Here is an 8 by 8 square that has been divided into four pieces:

 

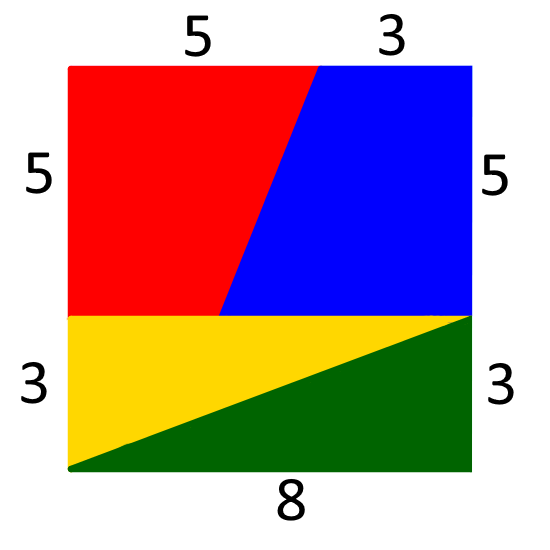
Here is a rectangle made from the same four pieces:
 

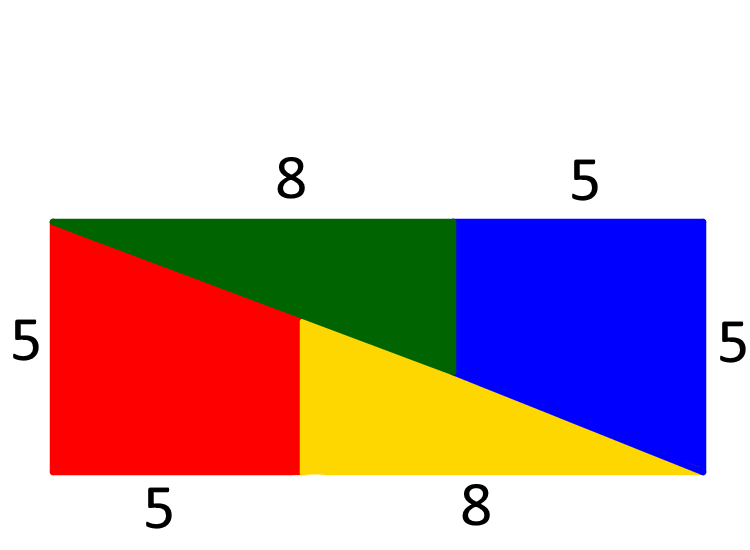
You might like to try cutting out the shapes from a piece of paper.

It seems that the same pieces can make two shapes with different areas!
Can you explain where the extra area comes from?


Here are some questions you might like to consider:

Can other squares be split up and rearranged to make rectangles with a different area?

Are there other square/rectangle pairs where the areas differ by 1 square unit?

Is there a pattern in the sizes of squares that can be arranged in this way?