Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
All Wrapped Up
Age 7 to 11
Challenge Level 





Well, we're often wrapping up presents - I find that many of them arrive in boxes that are cuboid. Remember those? A cuboid has 6 faces; each face a rectangle (including squares); each face paired with one the same on the opposite side and all the angles 90 degrees. So they might look like these:
Now let's talk about the wrapping paper. You are probably used to using A4 paper for all kinds of things. A4 paper looks a bit like this:

But two A4s together make A3:
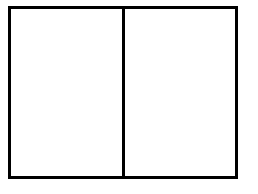
So we have:

Which could look better as:

Now for easiness we'll approximate the size of the A3 sheet to 40cm by 30cm.
The wrapping paper we'll be using is A3-size, like the picture above.
So, we're wrapping up a cuboid in this A3 wrapping paper.
The challenge is to find the largest cuboid that can be covered completely with the A3 sheet - you will probably want to stick to whole numbers of centimetres!
Rather than wrapping the cuboid like we might do a birthday present, let's think about it as if we're trying to have as little overlap as possible.
You might do this practically or you may use diagrams or even a spreadsheet - it is up to you.