Brush Loads

Callum and Josh submitted some ways of making the largest number of strokes and the smallest number of strokes for 5, 6 and 7 cubes:

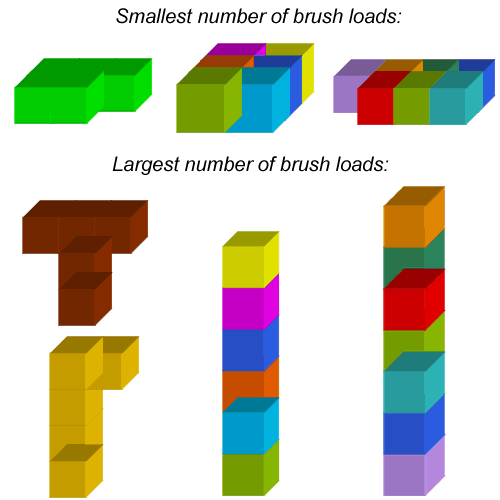
Lan explored the pattern for greater numbers of cubes, as did Rohaan from New Zealand. Lan describes the method used:

From counting cubes, we find:
With 5 cubes, the least number of BLs is 15, and the largest number of BLs is 21.
With 6 cubes, the least number of BLs is 16, and the largest number of BLs is 25.
With 7 cubes, the least number of BLs is 19, and the largest number of BLs is 29.
With 8 cubes, the least number of BLs is 20, and the largest number of BLs is 33.
With 9 cubes, the least number of BLs is 23, and the largest number of BLs is 37.

We remark the pattern:
With 5 cubes, the least number is 15, and the largest number is 21.
With 6 cubes, the least number is 15+1 = 16, and the largest number is 21+4 = 25.
With 7 cubes, the least number is 16+3 = 19, and the largest number is 25+4 = 29.
With 8 cubes, the least number is 19+1 = 20, and the largest number is 29+4 = 33.
With 9 cubes, the least number is 20+3 = 23, and the largest number is 33+4 = 37.

This is interesting, isn't it? If we think about the least number of BLs, we are trying to make as close to a rectangular arrangement of cubes as possible. This helps us to see why we only add one face going from an odd to an even number of cubes, but three faces going from an even to an odd.

However, with is a rectangular array always the best for minimising the number of brush loads? If you had 9 cubes, how about making a square arrangement? How many brush loads of paint would you need then?

Rohaan then spotted that the largest number of strokes is always (4 x number of cubes) +1, and that the smallest number depends on whether the number of cubes is odd or even:

Odd: (n-5) x2 +15
Even: (n-6) x2 + 16

Does this work for a square arrangement too?