 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Brush Loads



We have five cubes and we're going to join them together, following a few simple rules:
- the cubes must be together face-to-face;
- they must not topple over.
We're going to paint the faces that can be seen. One Brush Load (a kind of unit that we'll use) will paint one square face.
For example, here are five cubes joined together:
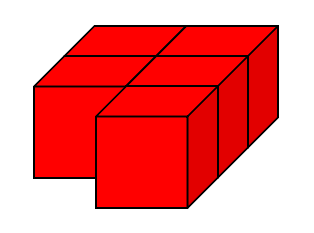
Counting the faces to be painted comes to 15, so 15 Brush Loads (or BLs) are needed. Remember we're only counting visible faces, so not those that are touching the surface where the cubes are placed.
But of course we could have placed the five cubes differently, for example:

Counting the faces to be painted now, we have 17, so 17 BLs.
Can you find ways of arranging five cubes so that:
- you need as few BLs as possible?
- you need as many BLs as possible?
Can you find arrangements that need all the numbers between the largest and the smallest numbers of BLs?
What happens if you use more cubes, for example 6, 7, 8...?
Can you find out the smallest number of BLs and the largest number of BLs possible in each case?
Can you predict the arrangements which need as few BLs as possible and as many BLs as possible?
You may also like
The Big Cheese
Investigate the area of 'slices' cut off this cube of cheese. What would happen if you had different-sized block of cheese to start with?
Wrapping Presents
Choose a box and work out the smallest rectangle of paper needed to wrap it so that it is completely covered.