Tables Without Tens

You will need a piece of squared paper for this activity. If you don't have any, you can get a sheet here.

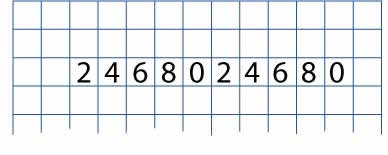
Write the ones digits of the numbers in the two times table from $1 \times 2$ up to $10 \times 2$ in a line. Leave some room at the top of the paper, and some space to the left and right, a bit like this:

You might be able to see some patterns in these numbers.

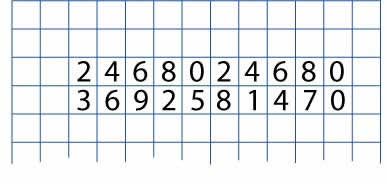
Now, do the same thing with the multiples of three. Remember, just write the ones digits, this time directly underneath the line of the two times table, like this:

 

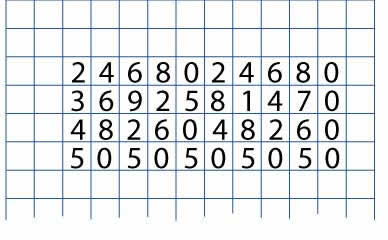
Continue by writing in the four and five times tables in the same way. Again, just using the ones digits.

 

Now look at the whole array of numbers you have created.

What patterns can you find?

Try to explain why the patterns occur.

What do you notice about these four sets of numbers?

Can you predict what would happen next if we wrote in the next times table?

 

***************

 

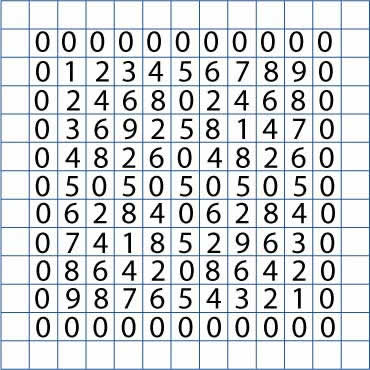
Well, why not add in the tables of sixes, sevens, eights, nines and finally tens?

 

After that, for the sake of completeness, we could put in the table of ones and zeros.

Do you have a grid that looks like this?

 

 

What patterns are there here?

What about repeats?

Can you predict what you will find?

How might you record the repeats that you find?

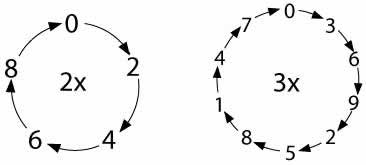
Each line could be written like this:

 

 

But you will probably find some other ways which are just as good.

You could try writing all the tables like that.

Are some tables the same or similar to others?

Does it matter which way the arrows go?

What can you discover about the pattern of repeats?

Can you predict what you will find out about 'pairs' of tables?

Why do this problem?

This problem involves learners noticing patterns, and making and proving conjectures. It is, incidentally, also an engaging way of revising multiplication tables! In addition, it is also very useful for encouraging learners to predict what they think they will find out.

Possible approach

You could introduce the investigation by inviting the class to help you record the ones digits of the two times table on the board. You may like to pause with just that row of digits written up, and invite learners to comment on anything they notice. Can they explain the pattern of digits?

Complete the ones digits of the three times table in a similar way, directly underneath the two times table, so that learners get a feel for the task. Encourage them to work in pairs from there so that they are able to talk through their ideas with a partner. Have plenty of squared and plain paper available. (Squared paper can be found here.)

Once they have completed the ones digits of the four and five times tables, draw everyone together again and ask whether they notice any patterns. Invite them to talk to a partner about their noticings, and then encourage everyone to share them with the whole group. Say that mathematicians aren't satisfied with noticing patterns, although that is a great start, we want to know why the patterns occur. Set the class off again, inviting them to choose a pattern they have noticed and try to explain why it occurs. 

As they work in pairs, listen out for those children who are drawing on what they know about the number system to explain a noticing. You could warn a few pairs that you'd like them to share their explanations with the whole class in the final plenary.

If you are able, you could extend this task further to look at the zero, one, six, seven, eight, nine and tens times tables, as is suggested.

Key questions
 

Possible support

Some learners will find it helpful to use a standard $10 \times 10$ 'table-square' to help with the tables. The resulting ones-numbers can then be transferred to a plain sheet of squared paper. This ready-made sheet might help.

Possible extension