You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?
Age 14 to 16
Challenge Level
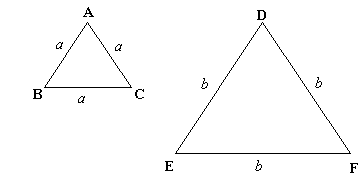
ABC and DEF are equilateral triangles of side 3 and 4 respectively. Construct an equilateral triangle whose area is the sum of the area of ABC and DEF .
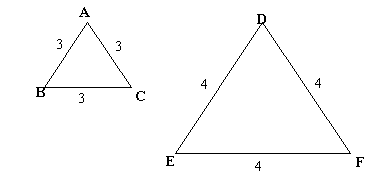
Does this work for any whole number side lengths?
If not, under what circumstances does it work?
What if the lengths of the sides of the triangles had been a and b instead of 3 and 4?
Can you construct an equilateral triangle whose area is the sum of the areas of ABC and DEF? What is the new area?
NRICH is part of the family of activities in the Millennium Mathematics Project.