Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Gold Yet Again
Age 16 to 18
Challenge Level 





Nick Lord says that this problem is immediately enticing for students (and for him) and there are many possible approaches to explore and compare.
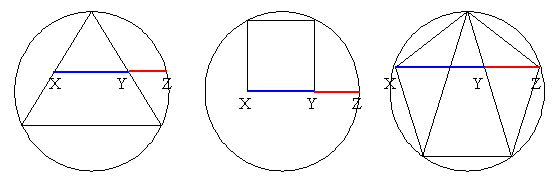
In the equilateral triangle inscribed in the circle, $X$ and $Y$ are the midpoints of the edges. Find the ratio${XZ\over XY}$.
The square sits on a diameter of the circle. Find the ratio ${XZ\over XY}$.
The regular pentagon is inscribed in the circle. Find the ratio ${XZ\over XY}$.
See also the problem Gold Again.