Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Running Race
Age 14 to 16
ShortChallenge Level 





- Problem
- Getting Started
- Solutions
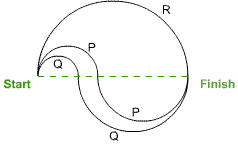
All three runners finish at the same time.
Let the radius of $R$'s track be $r$ and let the radius of the first semicircle of $P$'s track be $p$; then the radius of the second circle of this track is $r-p$.
The total length of $P$'s track is $\pi p + \pi(r-p) = \pi r$, the same length as $R$'s track.
By a similar argument, the length of $Q$'s track is also $\pi r$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Giant Holly Leaf
Find the perimeter and area of a holly leaf that will not lie flat (it has negative curvature with 'circles' having circumference greater than 2πr).
Contact
A circular plate rolls in contact with the sides of a rectangular tray. How much of its circumference comes into contact with the sides of the tray when it rolls around one circuit?