Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Running Race
Age 14 to 16
ShortChallenge Level 





- Problem
- Getting Started
- Solutions
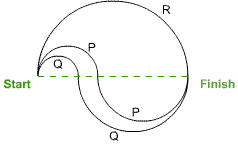
In a leisure park there are three running tracks, all with the same Start and Finish, and all made from either one or two semicircles with centres on the same line.
Three runners $P$, $Q$ and $R$ start together at the Start and run at the same constant speed along the tracks shown. In what order do they finish?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.