 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Triangle Animals



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Triangle Animals
I can join two equilateral triangles together along their edges like this:
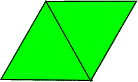
How many different ways are there to join three equilateral triangles together? (You must match an edge to an edge.)
How do you know you have got them all? You may find it useful to print out and cut up triangles from this sheet.
Have you got a system for checking that you have them all?
For a further challenge, you might like to look at Tri-Five.
Why do this problem?
Possible approach
Key questions
Possible extension
Children could have a go at Tri-Five. They could also see what happens if they use two or three isoceles triangles. Are their results different? Why? Again the focus should be on developing the use of accruate descriptive language and beginning to introduce the correct mathematical vocabulary of vertices, sides and angles.
Possible support
Having lots of cut-out triangles for children to stick down will help them access this challenge. You could use this sheet of equilateral triangles for printing and cutting (and possibly laminating too).