Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Symmetric Trace
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Pranav from Vardhana School had a good
suggestion : copy the image from the NRICH webpage into Paint and
then make a copy you can rotate and compare.
Also if you copy into Word, and rotate a copy, you could use one of the drawing tool to trace over one of the curves you want to compare and then move that new line around to see if it fits over the rotated copy.
Trace 2 does not line up with itself upside down. This can be spotted by looking at the lowest point on the line, the curve is sharper than at the highest point on the line, and so when rotated these two can not line up.
Trace 3 on the other hand does line up with itself upside down. This can be spotted by the fact that when you rotate the graph and slide it along it lines up. Another method is to draw a line at the top:
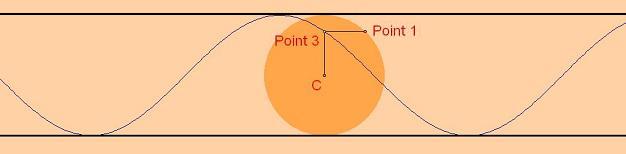
You can now notice that when the wheel has turned 180 degrees, then the rotated diagram is the same as the one above, and so the rotated graph does line up with itself.
Also if you copy into Word, and rotate a copy, you could use one of the drawing tool to trace over one of the curves you want to compare and then move that new line around to see if it fits over the rotated copy.
Trace 2 does not line up with itself upside down. This can be spotted by looking at the lowest point on the line, the curve is sharper than at the highest point on the line, and so when rotated these two can not line up.
Trace 3 on the other hand does line up with itself upside down. This can be spotted by the fact that when you rotate the graph and slide it along it lines up. Another method is to draw a line at the top:
You can now notice that when the wheel has turned 180 degrees, then the rotated diagram is the same as the one above, and so the rotated graph does line up with itself.