Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tessellating Hexagons
Age 11 to 14
Challenge Level 





This problem follows on from some of the ideas in Tessellating Triangles and Tessellating Quadrilaterals. It was inspired by a problem in "Tiles and Tiling", an activity book published by the Association of Teachers of Mathematics.
Here is a tessellation of regular hexagons:
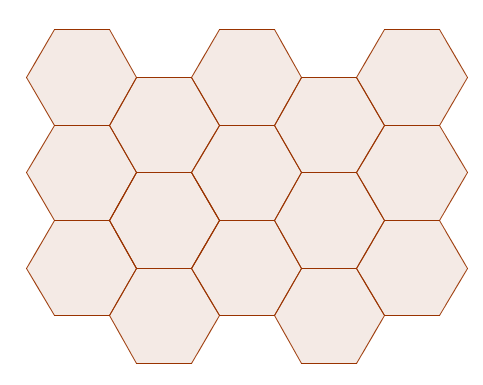
Can you explain why regular hexagons tessellate?
What about a hexagon where each pair of opposite sides is parallel, and opposite sides are the same length, but different pairs of sides are not the same length?
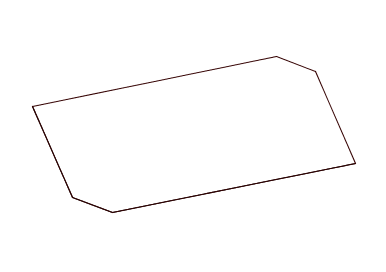
You can print off some square dotty paper, or some isometric dotty paper, and try drawing hexagons of this form on it. You could also draw some hexagons using this interactive. Can you tessellate them?
Do all hexagons of this form tessellate? How do you know?
Now let's consider hexagons with three adjacent angles which add up to $360^{\circ}$, sandwiched by two sides of equal length, as in the diagram below:
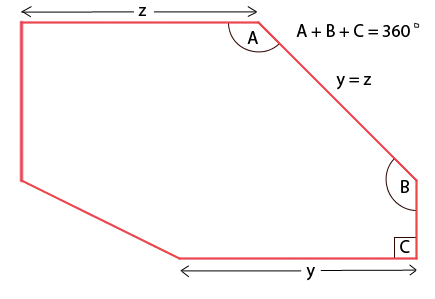
Is it true that any hexagon of this form will tessellate? How do you know?
Click below for a hint that might help you get started.
You could start by convincing yourself that sides $y$ and $z$ are parallel...
Can you find a hexagon which doesn't have a pair of equal parallel sides, but still tessellates?