Produced by Henry Kwok

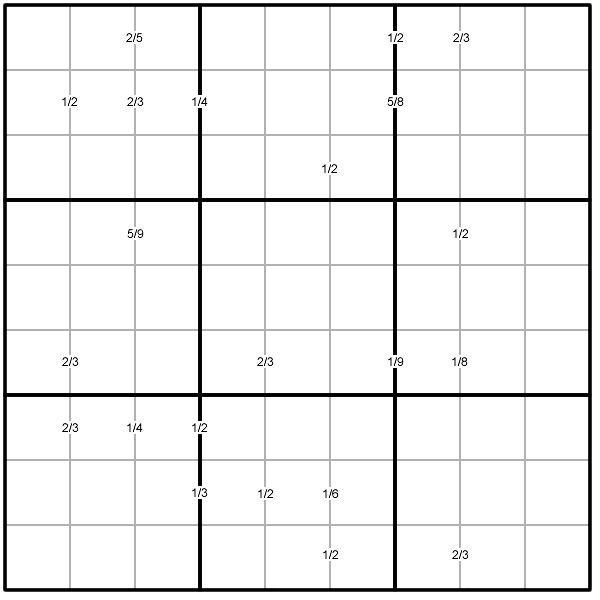
Basic Rules of "Ratio Sudoku"

The special clue-numbers in this Sudoku variant are fractions or ratios in the lowest terms, hence the name for the puzzle.

The clue-numbers are always placed on the border lines between selected pairs of neighbouring cells of the grid.

Each clue-number is the fraction of the two numbers in adjacent cells (to the left and right). Each fraction is written in its lowest terms, with the smaller number denoted as the numerator. Thus $1/2$ can stand for the following combinations of numbers in the two adjacent cells: $1$ and $2$, $2$ and $1$, $2$ and $4$, $4$ and $2$, $3$ and $6$, $6$ and $3$, $4$ and $8$, $8$ and $4$.

When fractions are placed on consecutive border lines, a number of combinations are possible. For example:

• if two fractions, $2/3$ and $1/4$, are placed consecutively from left to right, the possible combinations of answers in the three neighbouring cells would be the following two sets of numbers $3$, $2$ and $8$, or $6$, $4$ and $1$;

• if three fractions are placed on the consecutive border lines in the following order $2/3, 1/4$ and $1/2$, the combinations of answers in the four neighbouring cells would be $3, 2, 8$ and $4$, or $6, 4, 1$ and $2$.

The remaining rules are as in a "standard" Sudoku, and the object of the puzzle is to fill in the whole $9 \times 9$ grid with numbers $1$ through $9$ (one number per cell) so that each horizontal line, each vertical line, and each of the nine $3 \times 3$ squares (outlined with the bold lines) must contain all the nine different numbers $1$ through $9$.