Copyright © University of Cambridge. All rights reserved.
'Two Clocks' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem can help children understand that the analogue clock is really two scales superimposed on each other. This is what makes it so difficult for children to read. Focusing on the hands separately will help children understand what each one indicates. The novel context of this problem could provide a
good assessment opportunity.
The problem lends itself to collaborative working, both for children who are inexperienced at working in a group and children who are used to working in this way. By working together on this problem, the task is shared and therefore becomes more manageable than if working alone.
Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.
Possible approach
Before tackling this problem, children will need experience of reading analogue clocks. It would be helpful to have a large demonstration clock available to use with them and of course referring to a 'real' clock on the wall of the classroom might also be useful. Alternatively (or as well), you could make use of an interactive version on your whiteboard.
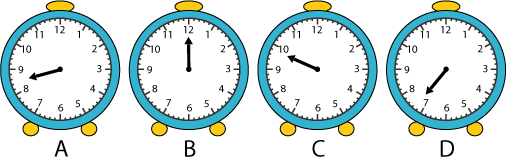
Ask the children to work in pairs on the first part of the problem so that they are able to talk through their ideas with a partner. This sheet contains two copies of the four clock faces. Once they have had chance to solve it, bring the group back together and allow
them to explain how they reached their conclusions. You might expect quite sophisticated reasoning from some children, which also indicates some understanding of why the hand is at the point it is between two digits. You can always demonstrate the movement of the hands using a real or virtual clock.
The combination of 'real-life' reasoning and telling the time makes the second part of the problem quite a challenge. So, ask two pairs to join together to make groups of four. Allocating these clear roles (Word, pdf) can help the group to work in a purposeful way - success on this task could be measured by how effectively the group members work together as well as by their final solution. This version of the
roles has been adapted for primary children.
Introduce the four group roles to the class. It may be appropriate, if this is the first time the class has worked in this way, to allocate particular roles to particular children. If the class works in roles over a series of lessons, it is desirable to make sure everyone experiences each role over time.
For suggestions of team-building maths tasks for use with classes unfamiliar with group work, take a look at this article and the accompanying resources.
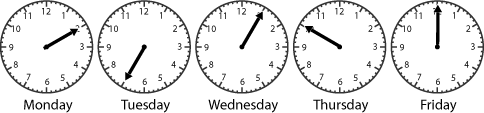
Give each group of four this sheet, which summarises the second part of the problem. You could also give them these twelve cards, five of
which have the clock faces on them and five of which give the information about each day of the week. Challenge them to work on the task in their groups so that they can match the clock face with the day. Explain that you will expect them to report back at the end of the session and at that point you will be looking out for good explanations of how they went about the task. Give each group a
large sheet of paper on which to record notes for feeding back, including any questions that they may have as a result of having had a go at the task.
There are many ways that groups can report back. Here are just a few suggestions:
- Every group is given a couple of minutes to report back to the whole class. Learners can seek clarification and ask questions. After each presentation, children are invited to offer positive feedback. Finally, pupils can suggest how the group could have improved their work on the task.
- Everyone's posters are put on display at the front of the room, but only a couple of groups are selected to report back to the whole class. Feedback and suggestions can be given in the same way as above. Additionally, children from the groups which don't present can be invited to share at the end anything they did differently.
- Two children from each group move to join an adjacent group. The two "hosts" explain their findings to the two "visitors". The "visitors" act as critical friends, requiring clear mathematical explanations and justifications. The "visitors" then comment on anything they did differently in their own group.
Key questions
If your focus is effective group work, this list of skills may be helpful (Word, pdf). Ask learners to identify which skills they demonstrated, and which skills they need to
develop further; or ask them to identify someone else in the group who demonstrated a particular skill.
If your focus is mathematical, these prompts might be useful:
What does that hand tell you?
What time could the clock be showing? How do you know?
Roughly, what could the time be on Monday/Tuesday etc?
Which three clocks show minute hands five minutes apart?
How might that help you to decide which days they were?