Copyright © University of Cambridge. All rights reserved.
'Pebbles' printed from https://nrich.maths.org/
Show menu
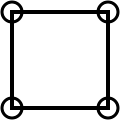
Imagine that you're walking along a sandy beach collecting pebbles. You start off with four pebbles and you place them on the sand as the corners of a square. The area inside your pebbles is just 1 square.
|
|
|
|
|
|
|
|
|
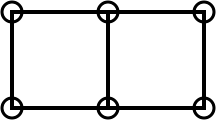
By adding another 2 pebbles you double the area to 2 squares, like this:
|
|
|
|
|
|
|
|
|
|
||
The rule is that you keep the pebbles that you already have, not moving them to any new positions, and add as few new pebbles as necessary to double the previous area.
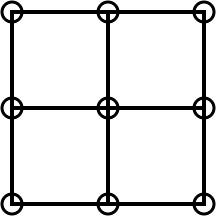
So, to continue, we add another three pebbles to get an area of 4:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
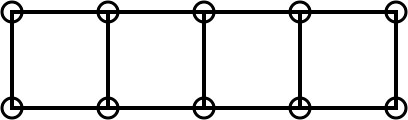
You could have doubled the area by doing this instead:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
But this would not be allowed because we are adding as few pebbles as possible each time.
The sixth arrangement of pebbles would look like this:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Now it's time for you to have a go.
What do you notice about the arrangements? What questions could you ask about them?
You might like to explore:
How many extra pebbles are added each time? This starts off as 2, 3, 6...
How many are there around the edges? This starts off as 4, 6, 8...
How big is the area? This starts off as 1, 2, 4...
How many pebbles are there inside each arrangement? This starts off as 0, 0, 1, 3, 9...
Don't forget the all-important question to ask - "I wonder what would happen if I ...?''
More Pebbles is a three-dimensional version of this task, which you might like to have a go at afterwards.