Here is one of the magic labellings of the W shape from Magic W problem with a magic total of $14$ on each of the four lines making the W shape.

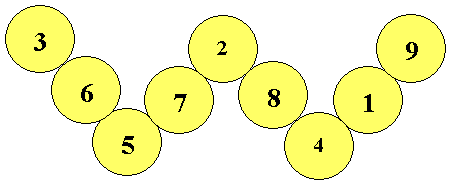
Prove that for every labelling with a magic total $T$ there is a corresponding labelling with a magic total $30-T$.

Find the values of $T$ for which magic labellings exist and show that there are a total of $12$ magic labellings altogether.

Note that two labellings are considered to be the same if they are reflections of each other or if the two numbers at the ends of the outside legs are interchanged.