Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Whirlyball
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Andrei from Tudor Vianu National College, Bucharest, Romania and Shaun from Nottingham High School both sent in excellent solutons to this problem.
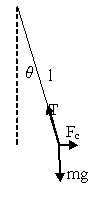 |
After drawing the picture, I observed that the forces
(the gravitational force acting on the ball, the tension in the wire and the
centrifugal force) keep the body in equilibrium. Considering the
centrifugal force, I work in a non-inertial frame of reference,
i.e. in the frame centred on the ball, which is in an
accelerated movement in respect to Earth.
In terms of the vectors we have $$m g + F_c + T = 0.$$
|
Resolving horizontally and vertically and using $F=ma$ (where $a$ is the acceleration towards the centre and $T$ is the magnitude of the tension in the string):
$$
\begin{align}
T\cos \theta &= mg\\
T\sin \theta &= ml\sin \theta \omega^2\;.
\end{align}
$$
Eliminating $T$: $$l\omega^2 \cos \theta = g$$ and hence the angle $\theta$ is $\cos^{-1}{g\over l\omega^2}$.
I know that $\cos^{-1}$ is a decreasing function in the interval of interest for the problem. As $\omega$ increases, the angle $\theta$ also increases and the whirling ball rises up, the radius of its circular path also increasing.
The ball can whirl in a circle while $\theta > 0$. So, as I explained above, to find the smallest angular velocity, I have to find the smallest angle. For $\theta \to 0$, ${g\over l\omega^2}\to 1$ and so $$\omega \to \sqrt {g\over l}.$$ This is the smallest angular velocity with which the ball could rotate in a circle.
The period of this movement is: $$T = {2\pi \over \omega} = 2\pi \sqrt {l\over g}.$$ It is interesting to observe that this is also the period of isochronal oscillations of the mathematical pendulum, i.e. the period of oscillation of a material point of mass $m$ attached to an inextensible string without mass deviated from the vertical by angles less than $5^\circ$.