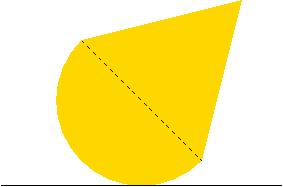
A solid hemisphere of radius $a$ and a solid right circular cone of height $h$ and base radius $a$ are made from the same uniform material and joined together with their circular faces in contact. Find the position of the centre of gravity of the whole body.

If the body is placed on a horizontal table with its hemispherical surface in contact with the table in what position will it come to rest if (i) $h=a$ and (ii) $h=2a$?

(iii) If the body always rests in equilibrium when it is placed on a horizontal table with a point of the hemispherical surface in contact with the table find $h$ in terms of $a$ and the angle of the cone in this case.

(iv) In what position does the body rest in equilibrium for other angles of the cone (other values of $h/a$) and when will the equilibrium be stable?