Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Roll On
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
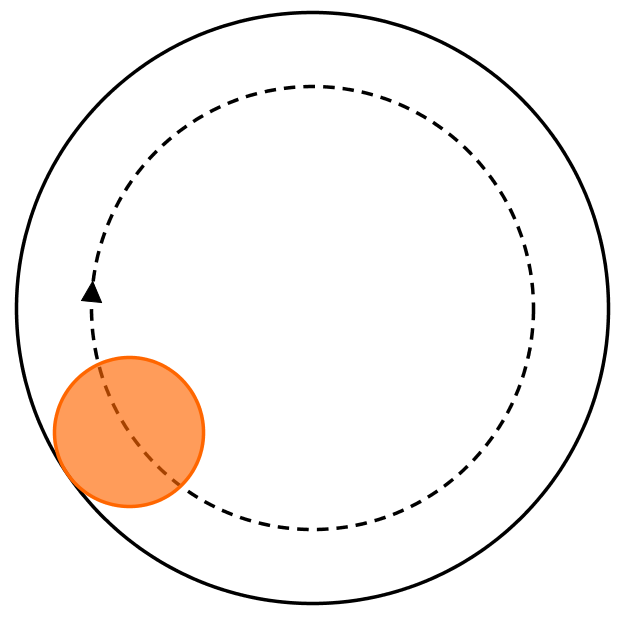
A circular disc of diameter $d$ rolls without slipping around the inside of a ring of internal diameter $3d$, as shown in the diagram. By the time that the centre of the inner disc returns to its original position for the first time, how many times will the inner disc have turned about its centre? What if the disc rolls around the outside of the ring?
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
Circumspection
M is any point on the line AB. Squares of side length AM and MB are constructed and their circumcircles intersect at P (and M). Prove that the lines AD and BE produced pass through P.