 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2005 Revised 2012
Taking Chances Extended
This article first appeared on MOTIVATE.
An introduction to the topic
This article is mainly about probability , the mathematical way of looking at random chance. The ideas and applications of probability are widespread: it is the foundation of the science of statistics, it influences decision-making in business (and even in sport), it helps us understand the way diseases spread and can be controlled, and the patterns of catastrophes such as earthquakes or transport accidents. Plainly, it applies to studies of Lotteries, and other games involving coins, cards or dice.
I shall use games of chance to illustrate ideas of probability, but I am NOT suggesting that you play any particular game. Indeed, the more you know about probability, the better you appreciate the odds against you in "commercial" games. I have never bought a ticket in the UK National Lottery, I belong to no casino, my bets on horses are small and rare.
Even before Roman times, soldiers used bone dice in various games to help pass the time on long campaigns, but the first systematic studies of how chance works were made in the sixteenth and seventeenth centuries. For example, gamblers wanted to know the chances for the different totals when three dice are thrown. Pascal and Fermat considered the following problem ("the problem of points"):
"Annie and Boris play a series of games, the winner will be the first to win a total of six games. But play must stop when Annie is leading 5-3. How best to divide the winning prize of 64 gold coins?"
One suggestion is to note that Annie is leading, so give her the prize of 64 coins, but that looks unfair to Boris. Another is to split the prize in the ratio 5:3, so that Annie gets 40 coins and Boris gets 24; but if this rule were used, then Annie would get all 64 coins if she were leading 5-0, 4-0, ..., even 1-0 at the time the game was stopped. Surely she should get more if she is leading 5-0, rather than 1-0? Another possibility is to say the game is not over, so split the prize equally - but that looks unfair to Annie. Pascal and Fermat asked: "If the series had continued, how likely is it that either player would have won, if each had an equal chance on any particular game?"
From the 5-3 score, after 3 more games we are sure to know who gets to 6 first. Write A or B to mean that Annie or Boris wins a game, and see that the only possible outcomes when the next three games are played are:
There are eight in this list, all equally likely if Annie and Boris have equal chances. In seven of these outcomes, Annie wins the series, and only one outcome (BBB) lets Boris win. Annie's winning chances are 7 in 8, Boris' chances are 1 in 8, they should split the prize 7:1. Annie gets 56 coins, and Boris gets 8 coins.
This solution was seen as fair to both players, and is probably the best answer to the question asked. It is not the only answer, and you will find that, in probability, there is sometimes room for lots of opinions. However, in many instances we all tend to reach the same conclusions.
For example, a common form of Lottery is that the winners are decided by how many people match a set of six numbers chosen from the list {1, 2, 3, ..., 49}. The intention of the organisers is that all individual numbers, and all number combinations, should have the same chance. They go to great lengths to make this happen: the Lottery balls are kept in secure boxes, at constant temperature, re-weighed before use, and handled with dry gloves. Despite these precautions, some people will try to assure you that combinations with obvious patterns, such as {1, 2, 3, 4, 5, 6} have a different chance from apparently more random combinations such as {2, 19, 31, 32, 44, 46}, but studies of Lotteries worldwide never find convincing evidence for such beliefs. The evidence is consistent with the notion that the Lottery organisers achieve their objective: all the permitted choices have the same chance.
In that case, we find the chances of winning the various prizes by counting. Without going in to the details, there are nearly 14 million different ways of selecting six numbers from the list {1, 2, 3, ..., 49}, so each ticket has about one chance in 14 million of winning a jackpot share. To get an idea of how small that chance is, think of buying TEN tickets a week: you will have to wait about 27 thousand years, on average, to win a share of the jackpot. Another counting exercise shows that there are just over 260 thousand combinations that match at least three of the winning set, and so win some prize. This means that any ticket has about one chance in 54 of winning something. Those who buy one ticket a week win, on average, about one prize a year (usually the smallest prize!).
Assume that all six sides on ordinary dice have the same chance. If you throw two dice, the total score can be anything in the range from 2 to 12, but the chances of the different totals vary widely. To see what these chances are, think of the dice as being easily distinguishable, say Red and Blue, and see how the totals can arise in the table below:
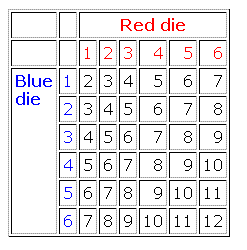
There are 36 entries in the table, all equally likely, so each entry has a chance 1/36. Now do some counting: the entries "2" and "12" appear once only, so their chances are 1/36. But "3" and "11" appear twice, so their chances are 2/36, while the chances for "4" or "10" are each 3/36, and so on. We find:
| Total | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Chance | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
(Do not bother to simplify fractions like 2/36 to make 1/18, it is easier to see the pattern without this step.)
This shows how easily unequal chances can arise, starting with equal chances. Anyone who plays games such as Monopoly, or Backgammon, where moves are based on the scores shown by two dice, can use this table to guide their play.
Averages
When you play a game lots of times, what happens on average is very important. If there are two possible rewards, 2 and 8, and they are equally likely, the average prize is 5. But suppose you tend to win 2 twice as often as you win 8. So your chances are 2/3 and 1/3 of winning 2 and 8. Your series of winnings might begin:
2 8 8 2 2 2 2 8 2 2 2 2 8 2 8 2 2 2 8 2 8 2 2 2
After a while, the 2s begin to dominate, and the average after a number of plays settles down to 4. The formula to find the average reward is to multiply each value by its probability, and add them all up .
In this example, when 2 and 8 each have probability 1/2, we have:
Average = 2 x (1/2) + 8 x (1/2) = 1 + 4 = 5
and when the probabilities are 2/3 and 1/3 we get:
Average = 2 x (2/3) + 8 x (1/3) = 4/3 + 8/3 = 4
As another example, if you get rewards 4, 6 and 18 with respective chances 1/2, 1/3 and 1/6 your average reward is:
4 x (1/2) + 6 x (1/3) + 18 x (1/6) = 2 + 2 + 3 = 7
Working out averages is one way of deciding whether a game is fair. If everybody makes their best play at each turn, and the average reward is the same for all, we could agree the game is fair. But if one player has a way of playing that leads to a higher reward, on average, than other players, even when they make their best plays, the game favours that player. (The player might have to exercise some skill to make this advantage felt.)
Games
Snakes and Ladders is a game with no skill at all as it depends entirely on luck. Many other games have a mix of skill and luck, and an understanding of probability can help you make the best of your luck. It can also help you see whether a game is fair to all players, or is set up to give one player an advantage. Sometimes, it is obvious whether or not a game is fair, and sometimes it is not at all clear - we have to work it out.
Coin matching games
You and your opponent each use an ordinary coin, Heads on one side and Tails on the other, to play a game. Each of you chooses whether to show H or T - you can do this how you like. For example, you might decide to show H every time, or to alternate H and T, or even to toss the coin, and let it make up its own mind. What each of you chooses, and how you choose it, is entirely up to you. When you have both made your choices, you simultaneously reveal your coins. If they are DIFFERENT (i.e., one of you chose H and the other T), you are the winner, but if they are the SAME (either both H or both T) your opponent is the winner. Is this a fair game? And what are your best tactics?
Actually, you don't yet have enough information to answer this, because I have not said what the rewards for winning are! First, assume that whichever of you wins gets a reward of 2 units (money, tokens, or whatever), and the loser pays the reward to the winner. So we can draw up a table of your "winnings", where +2 means you WIN two units, and -2 means you LOSE two units. The payoffs to you are:
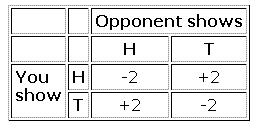
With this table, most people soon agree that the game is fair, so long as each player can keep their choice secret. If you KNEW what your opponent would show, you would obviously show the opposite; and if she knew what you would show, she would match your choice. But if your opponent has no idea what you will show, she is reduced to guessing. When she guesses right, she wins 2 units but when she is wrong, she loses 2 units. If either of you thoroughly mix up what you show - for example, you might privately toss the coin and show whichever side comes up - on average, you each win half the time. Since the rewards are equal, they cancel out, on average. Neither of you has an advantage.
Of course, one of you could be careless, and allow the other an advantage. If you tended to show more Heads than Tails, she could show Heads all the time, and so win more often than she loses (until you realise what she is doing, and change!). You can protect yourself against this by flipping your coin, and showing whatever comes up.
Although the game is fair, it is also a bit dull! So let's change the rewards so that the payoffs are:
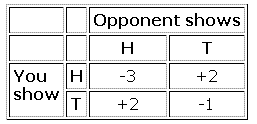
If you win, your reward is still 2 units, but if your opponent wins, you lose 3 when both of you show H, but you only lose 1 when both show T. Is this game fair?
I have heard people argue "No, it is not fair. You will show T all the time, so the opponent only wins 1, while you win 2", to which I respond "It would be silly of me to show T all the time, for she would notice, and also show T every time, winning one unit every game". Other people say "Yes, it is fair, because losing 3 or losing 1 will balance out winning 2, as in the last game." That sounds reasonable, but can we be sure that we shall lose 3 or lose 1 equally often? The more you look at it, the more you think the game might not be fair. There is clearly something to discuss, and argue about!
Actually, the game is NOT fair; you have a way of playing that enables you to win a small amount (1/8 of a token) on average, each play. You have no guarantee of winning any game, but if you use your best strategy, this small advantage will build up. After 8 games, you expect to be just one unit ahead, after 80 games you expect to be 10 units ahead, and so on. Your advantage is so small that your opponent might not even notice it, and be prepared to put their losses down to bad luck!
The game could be made fair, if you pay an entry fee of 1/8 unit per game to your opponent. (But one of the advantages of knowing some mathematics is that you can let your opponent discover this for themselves - if they are prepared to play without this entry fee, why should you worry!?) Why this game favours you, and how to take advantage of this, come after the next topic.
Randomising your choices
A very useful idea is to randomise your choice, i.e. mix up your choices at random to prevent your opponent being able to guess what you will do. Humans are not very good at doing this by just "thinking"! When they have said Heads several times in succession, they are more likely to say Tails next time - but previous choices should have no effect. We seem to need devices such as coins to help us randomise. A single coin does not remember what happened last time, it lets you use both choices equally often, and at random every time. But suppose you want to choose A and B at random, with A twice as often as B, on average?
You could use dice. Roll a single die,and choose A if the result is among {1, 2, 3, 4}, and B if it is either 5 or 6. In that way, you choose A twice as often as B, but your opponent cannot use the previous plays to work out what you will choose next time. You do not mind your opponent seeing that you are using a die to reach your choice, just make sure she does not see the score on the die!
Choosing A and B equally often, or one of them twice as often as the other, is fairly easy. But what if you want to randomise your choice between A and B, with chances of 4/15 for A and 11/15 for B? Here a pack of cards can be useful. You select 4 Red cards and 11 Black cards, and thoroughly shuffle them. When you are satisfied with the shuffling, look at the top card. If it is Red, choose A, if Black, choose B.
The table we found earlier, showing the chances of different totals for two dice, can also be useful. Try the effect of the rule:
Throw two dice. If the total is 5 or 6, choose A, otherwise choose B.
Overall, the chance of getting a total of either 5 or 6 is 4/36+5/36 = 9/36 = 1/4. We shall total either 5 or 6 on average one quarter of the time. So this rule would select A one time in four, and B three times in four (at random).
I can even use the stopwatch facility on my cheap digital watch to help randomise my choice! If I press the "stop" button after a few seconds, the time might be given as 5.92 seconds; the LAST digit is always among the list {0, 1, 2, ...,9}, and it seems reasonable to me that all ten of these possibilities are equally likely. (That is why I use the last digit, not the first one.) There are many ways (use ingenuity) of using these last digits to make a random choice, with a desired probability.
How to win at the Coin Matching game

Suppose you use the randomised strategy of showing H with probability 3/8, and T with probability 5/8. Look at the first column in the table, to see what happens when your opponent shows H. With probability 3/8, you lose 3 units, with probability 5/8 you win 2 units, so your overall average winnings are:
(3/8) x (-3) + (5/8) x (+2) = -9/8 + 10/8 = 1/8
Now look at the second column , to see what happens when your opponent shows T. This time, with probability 3/8 you win 2 units, while with probability 5/8 you lose just 1 unit. The overall average is:
Whatever your opponent does, you win 1/8, on average ! This game favours you. If you paid an entrance fee of 1/8 units each time, the game would become fair.
"Solving" this sort of game
To "solve" such a game is to find a way that you can play so that, no matter what your opponent does, you guarantee to win at least some amount, call it v (the value ), on average; AND to find a way that your opponent can play so that, no matter what you do, you cannot win more than this same amount v, on average.
In this last coin-matching game, we saw how you can win 1/8, on average, no matter what your opponent does. If your opponent also uses the same strategy as you - show H 3/8 of the time, T 5/8 of the time, at random - then your average winnings, whether you show H or T, are also 1/8. (You should check this!) You can guarantee to win 1/8, she can prevent you winning more than 1/8 . So we can now say we have solved this game, and its value is 1/8.
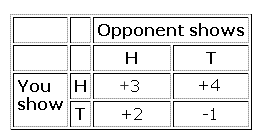
Suppose the set-up were:
A word of warning
In games like these, how well you do depends on what strategy your opponent uses. In all the games that we shall look at, there is some best strategy for both you and for your opponent. If either of you uses a best strategy, there is very little that the other can do about it. But also (and this is annoying!), if you assume she will use her best strategy, so you also use your best strategy, sometimes you get no advantage when she uses a worse strategy. Your own good play is protecting her against her folly!
For example, in the very first coin-tossing game where you either win or lose 2 units, suppose you decide to use your best strategy of randomly mixing H and T at equal frequencies. Then even if she lazily showed H every time, you win precisely zero, on average. Your good play does not lead to a profit, it just prevents a loss, whatever she does. You get no advantage from playing well. But if you find your opponent NOT using her best play, you might change your play to take account of what she is doing.
Suppose, in this same game, you notice your opponent mixes up H and T at random, but shows H 2/3 of the time, and T only 1/3. Then, when you use H, you "win"
on average, but when you use T you win
2 x (2/3) + (-2) x (1/3) = +(2/3),
on average. So if now you use T more often than H (while still mixing H and T randomly), you expect to get ahead.
Moral: work out your best play (and your opponent's). If your best play leads to a steady profit, you might as well stick to it; if your best play leads to a steady loss, negotiate an entrance fee. But if your opponent does not use her best play, you might be able to win by using a strategy that is different from what you would use if she did make her best play.
By the way: some games of this sort are much more complicated than the ones mentioned in this exercise, and the method that works for the games in this exercise will not work for ALL such games. So do not assume that perfect ability to deal with these games will let you solve all such games! (Sorry.)
Benford's Law
This leads to an entirely different sort of game. The first significant digit in the number 2.54 is 2; the first significant digit in 0.3937 is 3, the chance one ticket wins a share of the Lottery jackpot is 1/13,983,816 = 0.000000071511... - whose first significant digit is 7. Whatever number you think of, apart from zero exactly, its first significant digit, expressed as a decimal, will be among the list {1, 2, 3, 4, 5, 6, 7, 8, 9}. Will these nine alternatives occur equally often? Or are some of these numbers more likely than others to be a first significant digit?
You could invent some games to play against friends, based on this question. You win a point if the first significant digit is among {1, 2, 3, 4}, your friend wins a point if it is among {5, 6, 7, 8, 9}. Would that be a fair game? You may be surprised to find out that, very often, this game favours you , even though you only have 4 digits on your side, and your friend has 5.
The key question is: where do the data come from?
Here are some examples where the data will arise in a fairly arbitrary fashion:
- A World Atlas might list the countries in alphabetical order, and give, for each country, its area (in sq km, say), its population, and gross domestic product.
- A supermarket uses the bar codes to print off a list of how many of each item have been sold each week.
Other data arise in a more systematic fashion. For example:
- Car numbers are allocated in sequence.
- All (or most) telephone numbers in a certain area of town may begin with the same first digit.
- Seats in a theatre, cinema, soccer ground will be labelled A1, A2, A3, etc., in order.
Some data are deliberately random, for example:
- Computers and some pocket calculators are programmed to produce sequences of numbers such 0.74520778, 0.225189362, 0.01839284, ..., intended to be evenly scattered between 0 and 1.
| Brighton | 146 134 |
| Brinkworth | 1 139 |
| Bristol | 387 977 |
| Brixton | 1 030 |
| Broadstairs | 21 670 |
| Broadway | 2 503 |
| etc. |
Using just the first significant digit of these data led to the table:
| Initial Digit | Frequency |
| 1 | 32 |
| 2 | 19 |
| 3 | 13 |
| 4 | 9 |
| 5 | 9 |
| 6 | 9 |
| 7 | 4 |
| 8 | 1 |
| 9 | 4 |
| TOTAL | 100 |
This is very striking! It might be just a fluke, but the frequencies of the higher numbers are MUCH less than those of the lower ones.
This decreasing frequency for many lists of data was noticed over 100 years ago, by Simon Newcombe. His observation was ignored for over 50 years, and then rediscovered by Frank Benford in the late 1930s. Is there a pattern to the frequencies listed?
| Initial Digit | Values using 100 x LOG( ) |
| 1 | 30.1 |
| 2 | 17.6 |
| 3 | 12.5 |
| 4 | 9.7 |
| 5 | 7.9 |
| 6 | 6.7 |
| 7 | 5.8 |
| 8 | 5.1 |
| 9 | 4.6 |
| TOTAL | 100 |
Comparing the two tables, I hope you agree that the real data do seem to follow these values from this table fairly well. The frequencies in this second table are known as Benford's Law . An accountant, Mark Nigrini, has suggested using this Law as a check on whether people are fiddling their income tax returns. If the data are honest, he expects the figures on their tax returns to conform to Benford's Law, but if people have been inventing figures it is likely that some frequencies will stand out as "unusual", leading to a full investigation. Be warned!
And thinking about the "game" where you win if the first significant digit is one of 1, 2, 3, 4, if the data follow Benford's Law, you win nearly 70% of the time!
Now go back to the full original data, and notice that, for each number, you could shift the decimal point to get a number that is at least 1, and less than 10. So the population of Brighton, 146,134, becomes 1.46134; the population of Broadstairs, 21,670 becomes 2.167. If data contain values such as 0.00517, that would become 5.17, while 3.4056 would stay as it is.
In the data for 100 towns, the four towns whose populations had initial digit "7" would give rise to the numbers 7.43, 7.093, 7.2 and 7.96 when we make this adjustment. Add these up - this gives 29.683. Do the same for all nine blocks. My totals (rounded to 2 decimal places) are:
| Initial Digit | Frequency | Total |
| 1 | 32 | 46.44 |
| 2 | 19 | 44.31 |
| 3 | 13 | 46.95 |
| 4 | 9 | 39.62 |
| 5 | 9 | 48.62 |
| 6 | 9 | 58.35 |
| 7 | 4 | 29.68 |
| 8 | 1 | 8.94 |
| 9 | 4 | 36.86 |
(Here you can see that I have been honest with my data! I had been hoping that all the totals would be very nearly equal, but the "8.94" that arises from the one data point in class 8 spoils my hopes. Whenever you collect a sample of data, you are at the mercy of random chance, and I was unlucky that only one of my 100 towns had a population in class 8.) Mark Nigrini (mentioned above) had noticed that when data follow Benford's Law, these totals are often (roughly) equal. So let's refer to this as Nigrini's Law .