Try to visualise necklaces of touching circles centred at the vertices of a right-angled triangle, first where the circles touch on the sides of the triangle and then where points of contact lie on the sides produced. Now try to visualise where these circles meet the inscribed and escribed circles of the triangle.

Given any right-angled triangle $ABC$ with sides $a, b$ and $c$, find the radii of the three circles with centres at $A, B$ and $C$ such that each circle touches the other two and two of the circles touch on $AB$ between $A$ and $B$, two circles touch on $CA$ produced and two circles touch on $CB$ produced.

Now for any right-angled triangle $ABC$ find the radii of the three escribed circles as shown in the diagram.
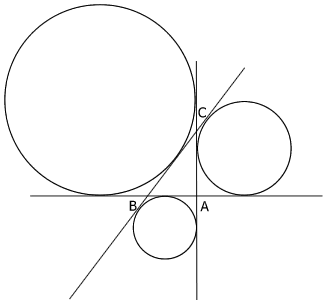