Copyright © University of Cambridge. All rights reserved.
'Olympic Magic' printed from https://nrich.maths.org/
Show menu
The Olympic emblem consists of five coloured rings which overlap to give nine regions. Here is a black and white diagram showing the overlaps:
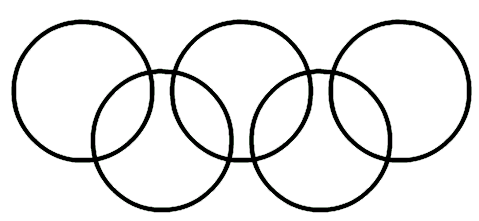
In order to contribute to a pension fund for the retiring International Olympic Committee people are asked to deposit money into each region.
The guidelines allow the delegate to take all the money in any one of the rings.
Place the numbers 1, 2, ... 9 in the nine regions so that the amount in each ring is the same. How many different ways can you find to do this?
(Problem from University of Sydney Mathematics Enrichment Groups 1999)
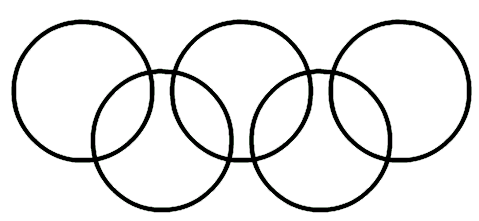
In order to contribute to a pension fund for the retiring International Olympic Committee people are asked to deposit money into each region.
The guidelines allow the delegate to take all the money in any one of the rings.
Place the numbers 1, 2, ... 9 in the nine regions so that the amount in each ring is the same. How many different ways can you find to do this?
(Problem from University of Sydney Mathematics Enrichment Groups 1999)