 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Stairs



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Here is a solution to STAIRS, which we very happily received from Hannah of West Flegg Middle School, Norfolk. She writes:
1.  |
2. 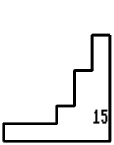 |
3.  |
4.  |
5.  |
6.  |
7.  |
8.  |
9.  |
10.  |
11.  |
12.  |
13.  |
14. 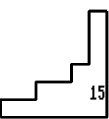 |
15.  |
16.  |
17.  |
18.  |
19.  |
20. 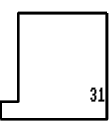 |
Biggest and smallest:-
This is my biggest
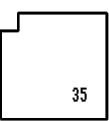
This is my smallest
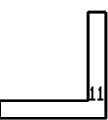
Then:-
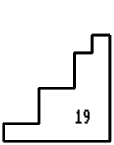
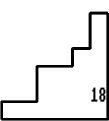
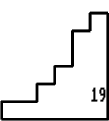
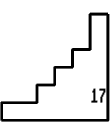
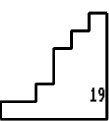
14 on the first sheet - No 19.
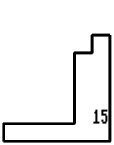
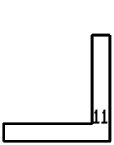
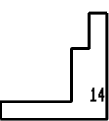
15 on the sheet - Nos. 14, 2, 3, 6.
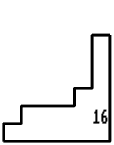
16 on the sheet - No. 9.
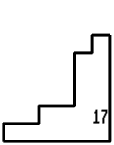
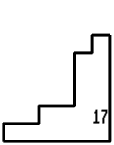
17 on the sheet - Nos. 8, 13, 18.
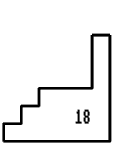
18 on the sheet - Nos. 4, 11.
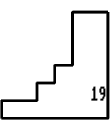
19 on the sheet - Nos. 1, 12, 13, 16.
22 on the sheet - No. 10.
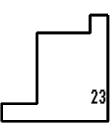
23 on the sheet - No. 17.
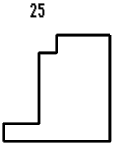
And so on... you can just add one to the last square, up the top if you like. I added them up at the top of the last three.
She went on to extend the challenge! WELL DONE
I wonder what would happen if it were 5 along and four up?
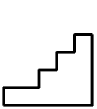
The amount would be smaller all the time but the method would be the same.
She also looked at 5 by 6 and 6 by 5. She finishes by saying:
I wonder what would happen if you could have two sets of steps?
e.g.,
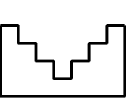
Bernard says "Well done, a good approach. I liked the way you had a go, then sorted them into an order, put in the missing ones, and saw how it was just going to go on. Then you asked a further question, and explored it a little. And you finished with a brand new question. Keep up this good work all of you!''