Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
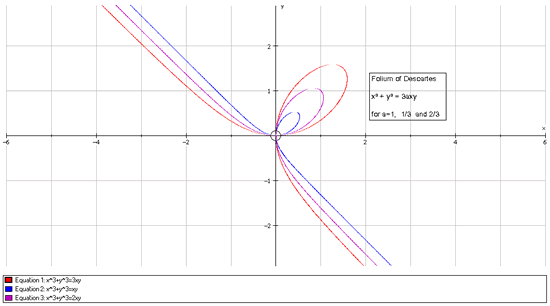
Folium of Descartes
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This excellent solution came from Marcos from Cyprus.
As I don't have any graphing software I'll be using the ideas in the question to sketch the graph at the end. I will try to give as detailed explanations as I can.
I'm assuming the constant $a$ is positive.
Firstly we show that the graph is symmetrical about $y=x$. How do we know if a graph is symmetrical about $y=x$? One simple approach is, if we change the $x-$ and $y-$axes round and plot it again we should get the graph looking as it did in the original case.
(To see this better, think of what happens when you 'fold' the $x-y$ plane along $y=x$).
Therefore, since we can swap the axes and preserve the shape this implies that we can just check if in our equation we can replace the $x$ with $y$ and the $y$ with $x$ and still get the same graph. This is obviously true:
$$x^3+y^3=3axy$$ goes to $$y^3+x^3=3ayx$$
which is the same thing. Thus, the graphs are symmetrical about $y=x$.
Using $y=tx$ in the equation, we get:
$$x^3 + t^3x^3 = 3atx^2.$$
When $x\neq 0$ and $t\neq -1$ we can divide by $x^2$ and $1+t^3$ and get
$$x={3at\over {1+t^3}},\quad y={3at^2\over {1+t^3}}.$$
To find a maximum point we can differentiate using the chain rule wrt $x$:
$$3x^2+3y^2{dy \over dx} = 3ay + 3ax{dy\over dx}.$$
Hence $${dy\over dx}= {{ay-x^2}\over{y^2-3a}}.$$
Now, the maximum is when $dy/dx = 0$, that is when $ay = x^2$. Using $y=tx$ gives $atx = x^2$ and when $x\neq 0$ this is at $x = 3at/(1 + t^3)$ so $1 + t^3 = 3$ and thus $t=2^{1/3}$ at the stationary point. Looking at the parametric form, this occurs at the point $(2^{1/3}a, 2^{2/3}a)$. Putting in an x-value just before and just after confirms the point to be a maximum.
(a) When $t$ is in $-\infty< t< -1$ from the parametric form of the equation $x$ must be positive and $y$ must be negative.
(b) When $t$ is in $-1< t< 0$ then $x$ is negative and $y$ must be positive.
(c) When $t$ is in $0< t< 1$ then $3at > 0$ and $t^3 > 0$ so $x$ is positive and so is $y$ but as $y = tx$ then $y < x$.
(d) Similarly when $t > 1$, $3at > 0$ and $1 + t^3> 0$ and so $x$ and $y$ are positive. As $y = tx$ then $x< y$.
For $t=-1$ the graph is undefined but as $t$ tends to -1 the absolute values of $x$ and $y$ get larger and the graphs get closer and closer to the asymptote $y = -x$.
One last aid to sketching the curve is the following. Is there a point such that $y=x$? Considering our equation, $2x^3=3ax^2$ at such a point. We already know (0,0) is on the graph so for other points we can divide by $x^2$. We get $x = y = 3a/2$ which corresponds to $t=1$. The important thing about this point is that considering our formula for $dy/dx$ if $x = y$ then $dy/dx = -1$ and so we know that at this point the gradient is that of the line $y = -x$. This tells us that (as the curve is symmetrical about $y = x$ and using parts (c) and (d) there is a 'loop' at this point.
Using all of this information, we conclude that a sketch of the graph looks something like this: