Each of the numbers $1$ to $15$ is used to label one of the vertices or one of the edges of this plum tree.

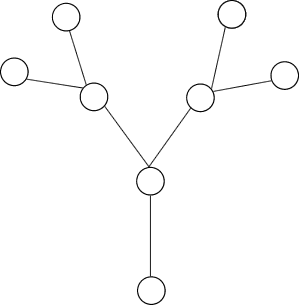
A graph is said to be 'vertex magic' if the sum of the numbers on a vertex and on all the edges joined to that vertex is the same for each vertex. We call this the 'magic sum'.

A graph is said to be 'edge magic' if, for each edge, the sum of the three numbers, on the edge and the two vertices at its ends, is the same. This is called the 'magic constant'.

A graph is said to be 'totally magic' if it is both vertex magic and edge magic. The labellings to make it vertex magic and to make it edge magic do not have to be the same and the magic sum and magic constant do not have to be the same .

Prove that this plum tree can be labelled to make it totally magic. Is there more than one edge magic labelling and more than one vertex magic labelling apart from symmetries and apart from simply exchanging the number on an extreme vertex with the number on its branch?

Can you construct a tree of your own that is totally magic?