Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Magic Caterpillars



- Problem
- Getting Started
- Student Solutions
Peter sent us this solution, using the starting point we gave:
There are $6$ vertices and $5$ edges. Let's suppose the magic constant is $S$ and this is the same at each vertex. The total of all the numbers $1 + 2 + ... + 11 = 66$ but the numbers on the edges, $a,b,c,d,e$ are counted twice. So, adding the magic sum at all six vertices:
$$(a+b+c+d+e)+66=6S$$
So $a+b+c+d+e$ is a multiple of $6$ and it is at least $1+2+3+4+5=15$ so it must be $18$ or more. Hence $6S\geq84$ and $S\geq14$.
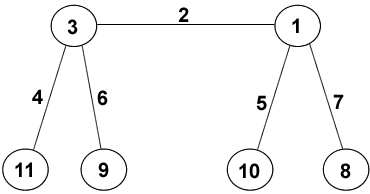
We're going to call the horizontal edge $e$, the front two edges $a$ and $b$, and the back two legs $c$ and $d$. Also, we see that the numbers $11$, $10$ and $9$ must all be in feet, as they're too big to be anywhere else.
Let's try $S=14$ first. We may as well take $a=3$, as the legs are all interchangeable at this stage.
Now if $b=4$, then we have $c=5$ (as the back legs are interchangeable). Also, we must have $d$ and the back foot as $6$ and $8$ (in some order), and we soon see that this isn't possible (as we'd also need $e$ plus the top left hip to add up to $7$). If $b$ isn't $4$, then we can assume that $c=4$. But similarly we find that we can't have $b=9$ or $b=8$ or $b=7$. So $S$ isn't $14$.
Let's try $S=16$. But then we need four pairs of numbers that sum to $16$ (one for each leg). We try: $(11,5)$, $(10,6)$, $(9,7)$, $(8,?)$ and we can't repeat the $8$ so that isn't possible.
So let's try $S=15$. This time, we may as well take $a=4$. There are only $4$ pairs that add up to $15$: $(11,4)$, $(10,5)$, $(9,6)$ and $(8,7)$. Call the number in the top left hip $f$.
If $b=5$, then we have $c=6$ and $e+f=6$, which isn't possible (as we don't have the right numbers left).
So we can take $c=5$. If $b=8$, have $e+f=3$ and then we'll need $f+g=4$, and this isn't possible. If $b=7$, have $e+f=4$ and we also have $f+g=4$ and this isn't possible either. Also we can't have $d=8$, as this is too big. So the only possibility is the one shown below (and this does indeed work).
(When I say the only possibility, of course the front legs could be switched, or the back legs, or the front and back swapped, but it's really the same caterpillar.)