In the Land of Trees all the caterpillars have numbers on their feet and hips (vertices) and on their legs and body segments (edges) as shown on this 4 legged caterpillar. All the whole numbers from 1 to $v+e$ are used where $v$ is the number of vertices and $e$ is the number of edges. Biologists classify them by their vertex-sums.

A vertex sum is the total of the numbers on the vertex and all the edges at that vertex.

The caterpillar shown has vertex sums:

11 (8+3), 13 (9+4), 15 (10+5), 17 (11+6), 25 (8+9+7+1) and 30 (7+10+11+2).
 

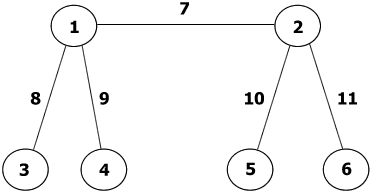
Show that one day a biologist may find a rare magic 4-legged caterpillar having the same sum at all its vertices and describe this creature.

Could there be two species of magic 4-legged caterpillars with different numberings?

Do magic 6-legged caterpillars exist?

What about magic caterpillars with even more legs?