Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cocked Hat
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
| Congratulations Aleksander from Gdynia Bilingual High School No3, Poland for your excellent solution to the Cocked Hat problem. As you will see, the solution hinges on simplification of an algebraic expression and solving a quadratic equation. |
Here is Aleksander's
solution.
First we will rearrange the expression from implicit to
explicit form. The given equation is
$$(x^2 + 2ay -a^2)^2 = y^2(a^2 - x^2)$$
Squaring the LHS gives
$$4a^2y^2 + 4ay(x^2-a^2) + (x^2 - a^2)^2 = y^2(a^2 -
x^2).$$
Collecting like terms gives the quadratic equation
$$y^2(3a^2+x^2)+ 4ay(x^2-a^2) + (x^2 - a^2)^2 = 0.$$
The discriminant is
$$\Delta = {16a^2(x^2 - a^2)^2-4(3a^2+x^2)(x^2-a^2)^2}= (x^2 -
a^2)^2(4a^2-x^2) = 4(a^2 - x^2)^3.$$
Solving this equation we get:
$$\eqalign{ y &= {-4a(x^2 - a^2)\pm \sqrt{4(a^2 -
x^2)^3}\over 2(3a^2+x^2)} \cr &= {(x^2-a^2)(-2a\pm
\sqrt{(a^2-x^2)})\over (3a^2+x^2)} }$$
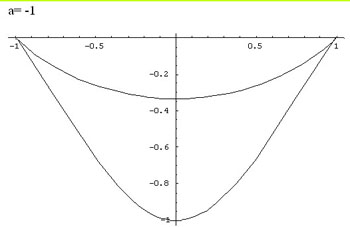
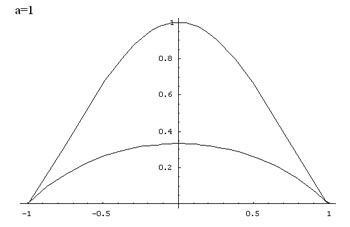
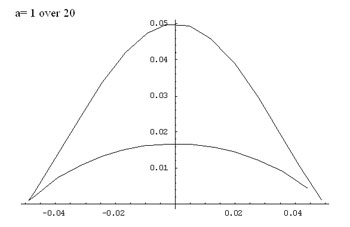
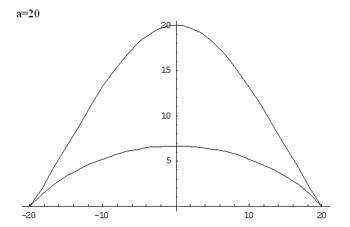
For each value of $a$ there are two branches of the graph
given by taking the +ve and -ve signs in this equation. Values of
$y$ are only defined for the interval $-a \leq x \leq a$. The
domain of $f(x)$ is $-a \leq x \leq a.$ The zeros of the function
are given by $x = a$ and $x = -a.$
Additionally, the function is symmetric with respect to the
y-axis, because $x$ always appears in even powers. Graphs for
parameters $a = n$ and $a = -n$ and are symmetric to each other
with respect to the x-axis, that is $y(n) = y(-n)$. Proof:
$$ {(x^2-n^2)(-2n\pm \sqrt{(n^2-x^2)})\over (3n^2+x^2)} =
-{(x^2-(-n)^2)(-2(-n)\pm \sqrt{(-(n)^2-x^2)})\over
(3(-n)^2+x^2)}$$
Here are some graphs of the function:
 |
 |
 |
 |
You may also like
Kissing
Two perpendicular lines are tangential to two identical circles that touch. What is the largest circle that can be placed in between the two lines and the two circles and how would you construct it?
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
Target Six
Show that x = 1 is a solution of the equation x^(3/2) - 8x^(-3/2) = 7 and find all other solutions.