Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Fractional Wall
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thanks to the many of you who submitted a solution to this problem. Congratulations to Josie, Dominic and George from St Nicholas CE Junior School, Newbury and also Abigail from Histon Junior School and Charlie from Beckley C of E who all sent in clearly explained solutions. The solution given below was sent in by Cong:
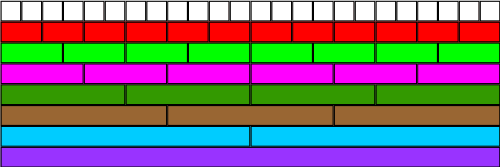
Using the image above, I can find $\frac{1}{2}$ as:
$1$ blue ($\frac{1}{2}$)
$2$ dark greens ($\frac{2}{4}$)
$3$ pinks ($\frac{3}{6}$)
$4$ light greens ($\frac{4}{8}$)
$6$ reds ($\frac{6}{12}$)
$12$ whites ($\frac{12}{24}$)
So I can also say that $$\frac{1}{2}= \frac{2}{4} = \frac{3}{6} = \frac{4}{8} = \frac{6}{12} = \frac{12}{24}$$
From the picture, I can find $\frac{1}{3}$ as:
$1$ brown ($\frac{1}{3}$)
$2$ pinks ($\frac{2}{6}$)
$4$ reds ($\frac{4}{12}$)
$8$ whites ($\frac{8}{24}$)
So I can also say that $$\frac{1}{3} = \frac{2}{6} = \frac{4}{12} = \frac{8}{24}$$
Again, using the image of the fraction wall, I can find $\frac{3}{4}$ as:
$3$ dark greens ($\frac{3}{4}$)
$6$ light greens ($\frac{6}{8}$)
$9$ reds ($\frac{9}{12}$)
$18$ whites ($\frac{18}{24}$)
So again I can say that $$\frac{3}{4}= \frac{6}{8} = \frac{9}{12} = \frac{18}{24}$$
The rule for working out equivalent fractions is to multiply the numerator and the denominator with the same whole number.