Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Diagonals for Area
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
Tom and James from Queen Mary's Grammar School, Walsall and Shu Cao from Oxford High School gave this solution for a convex quadrilateral. Can you see how to adapt the solution for the case of the arrow shaped quadrilateral?
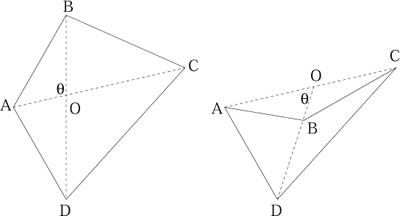
Suppose there is a convex quadrilateral $ABCD$, the diagonals
$AC$ and $BD$ cross each other at $O$. The angle between $AO$ and
$BO$ is $\theta$ degrees, the angle between $DO$ and $CO$ is the
same. The angle between $AO$ and $DO$ is $180-\theta$ degrees, the
angle between $BO$ and $CO$ is the same.
The area of triangle $AOB$ is ${1\over 2}AO\times BO \sin
\theta$.
The area of triangle $AOD$ is ${1\over 2}AO\times DO \sin
(180-\theta)={1\over 2}AO\times DO \sin \theta$.
The area of triangle $DOC$ is ${1\over 2}DO\times CO \sin
\theta$.
The area of triangle $BOC$ is ${1\over 2}BO\times CO \sin
(180-\theta)={1\over 2}BO\times CO \sin \theta$.
The area of the quadrilateral is the sum of these four
triangles.
$$\eqalign{ {\rm Area}&={1\over 2}AO\times BO \sin
\theta+{1\over 2}AO\times DO \sin \theta+{1\over 2}DO\times CO \sin
\theta+{1\over 2}BO\times CO \sin \theta \cr &= {1\over
2}[AO(BO+DO) + CO(DO+ BO)]\sin \theta \cr &={1\over 2}(AO\times
BD+ CO\times BD)\sin \theta \cr &={1\over 2}AC\times BD \sin
\theta }$$
So we have proved that for a convex quadrilateral the area of
the quadrilateral is given by half the product of the lengths of
the diagonals multiplied by the sine of the angle between the
diagonals.
You may also like
Biggest Bendy
Four rods are hinged at their ends to form a quadrilateral. How can you maximise its area?
So Big
One side of a triangle is divided into segments of length a and b by the inscribed circle, with radius r. Prove that the area is: abr(a+b)/ab-r^2