Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Triangle in a Triangle
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Jaydon from Newington College in Australia found the proportion for a triangle with base 12 units and height 9 units:
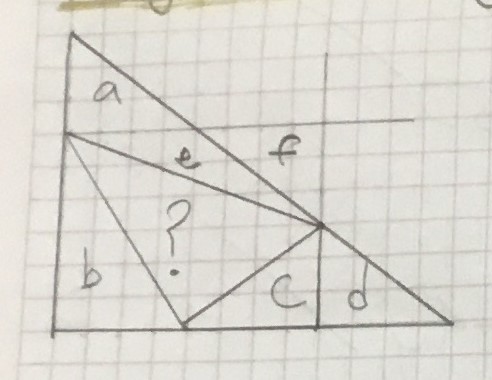 Formula to find shaded sections area:
Formula to find shaded sections area:? = whole $-$ a $-$ b $-$ c $-$ d $-$ e
whole = H$\times$B$\times\frac12$ = 9$\times$12$\times\frac12$ = 54
a = H$\times$B$\times\frac12$ = 3$\times$4$\times\frac12$ = 6
b = H$\times$B$\times\frac12$ = 6$\times$4$\times\frac12$ = 12
c = H$\times$B$\times\frac12$ = 3$\times$4$\times\frac12$ = 6
d = H$\times$B$\times\frac12$ = 3$\times$4$\times\frac12$ = 6
To find e:
Take e and f as one shape and do the formula as per usual, but then subtract {f from} the number you get from the formula to eliminate the section that is not part of the shape.
ef = 3$\times$8$\times\frac12$
12 $-$ f = e
12 $-\frac{3\times4}2$ = 12 $-$ 6 = 6
e = 6
Plug numbers into formula
? = 54 $-$ 6 $-$ 12 $-$ 6 $-$ 6 $-$ 6
? = 54 $-$ 36
? = 18
Ratio of ? to whole
= 18 : ?
= 18 : 54
= 1:3
Therefore as a fraction $\frac13$
Miranda and Sadaf from Greenacre Public School in Australia found a very simple solution to the general problem:
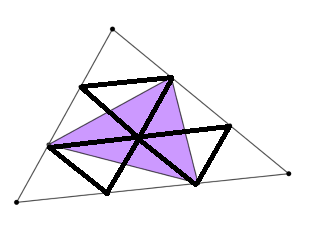 We looked at the second question part to see if we could find a pattern, and we did. We joined the dots to make 9 congruent triangles shown from the picture (1 at the top, 3 in the middle and 5 at the bottom). We then coloured in the purple-shaded triangle to work out the fraction out of 9. We saw that there were
six shaded halves of the triangles and converted that into three whole traingles. This was $\frac39$ of the triangle, simplified to $\frac13$.
We looked at the second question part to see if we could find a pattern, and we did. We joined the dots to make 9 congruent triangles shown from the picture (1 at the top, 3 in the middle and 5 at the bottom). We then coloured in the purple-shaded triangle to work out the fraction out of 9. We saw that there were
six shaded halves of the triangles and converted that into three whole traingles. This was $\frac39$ of the triangle, simplified to $\frac13$.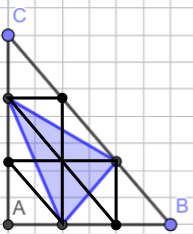 After finding the solution to the second problem, we tried the same strategy for the first part of this problem and it worked. It was harder to find how the smaller triangles would fit, but we soon found that 9 right angled triangles fit into the big triangle. We
shaded the blue area and this time it was harder to measure the fraction, but we looked closer and found that it was $\frac13$ as well.
After finding the solution to the second problem, we tried the same strategy for the first part of this problem and it worked. It was harder to find how the smaller triangles would fit, but we soon found that 9 right angled triangles fit into the big triangle. We
shaded the blue area and this time it was harder to measure the fraction, but we looked closer and found that it was $\frac13$ as well.So both solutions to the equations are $\frac13$.
Thomas from Davenies found a general solution to the problem with a right-angled triangle:
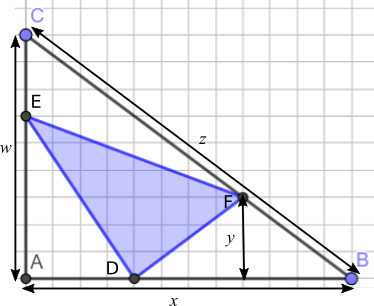 In triangle ABC, there is one shaded triangle. Let us call the shaded triangle (starting at the left bottom and going round clockwise) DEF. Hence the three unshaded triangles are AED, ECF and DFB.
In triangle ABC, there is one shaded triangle. Let us call the shaded triangle (starting at the left bottom and going round clockwise) DEF. Hence the three unshaded triangles are AED, ECF and DFB.Let us first work out the total area of triangle ABC. Let us call the line AB $x,$ the line CA $w$ and the line BC $z.$ The [vertical] line going down from F to $x$ (in the triangle DFB) is called $y.$ As point F is one third of the line $z,$ hence line $y$ is one third of the line $w.$ Therefore triangle ABC = $3xy\div2.$
Using this same logic, we can work out the area of the non-shaded triangles. Triangle AED = $\frac13 x\times 2y \div 2=\frac13xy$
Triangle ECF = $y\times\frac23 x\div 2=\frac13xy$
Finally, triangle DFB = $y \times \frac23 x\div2$
Added together, the three unshaded triangles = $xy.$ As the total triangle = $1.5xy,$ the area of the shaded triangle will thus be $0.5xy.$ Therefore the shaded triangle represents a third of the total area of ABC.
Steven from City of Sunderland College and Tommy from the Costello School, both in the UK, used trigonometry to find the areas in a general triangle.
Tommy's working is very clear, and shows in detail how the area of each triangle was found:
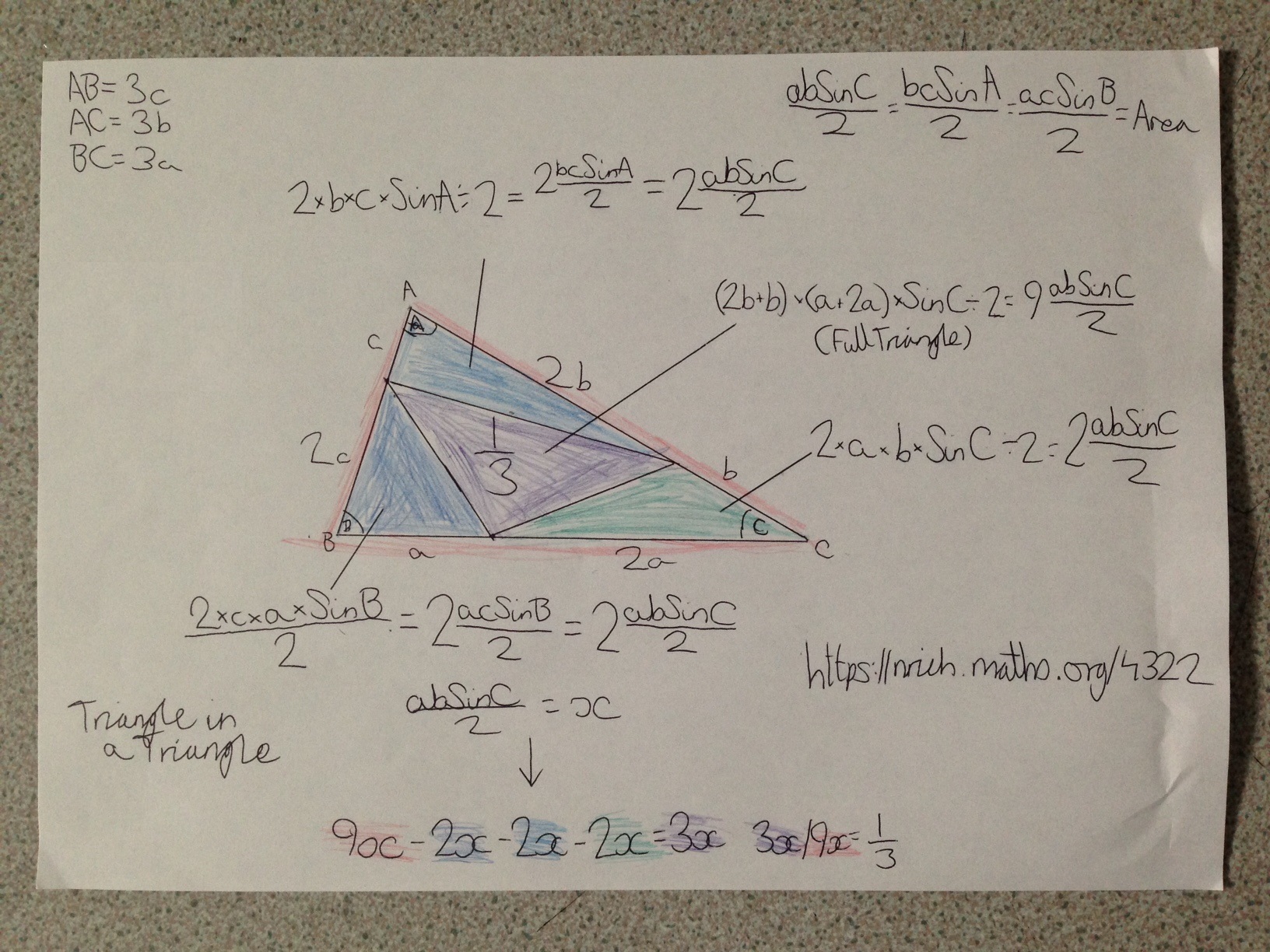
Steven used more algebra, and so in Steven's work, it is easier to see how this method is related to Thomas' method above:
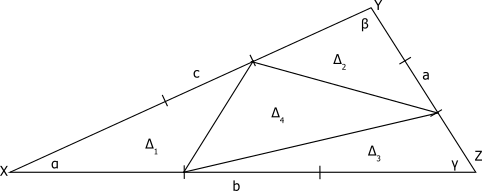
Let the area of triangle XYZ be $\Delta$, and the smaller triangles be $\Delta_1$ through $\Delta_4$, as above.
The area of the large triangle can be found as $\frac12bc\sin{\alpha}=\Delta$.
The proportions into which each side of the large triangle has been split means that, the base of $\Delta_1$ is $\frac13$ the length of the base of the large triangle, and the sloping side $\frac23$ that of the large triangle. So the area of $\Delta_1$ is $\frac12\frac b3\frac{2c}3\sin\alpha=\frac29\left(\frac12bc\sin\alpha\right)$. The same holds for triangles 2 and 3. So $\Delta_1=\Delta_2=\Delta_3=\frac29\Delta$
The area of the inner triangle, triangle 4, is therefore $\Delta-3\times\frac29\Delta=\frac13\Delta$.
Notice that, actually, it wasn't necessary to use trigonometry. Thomas' method can easily be extended to a general triangle.
 This relies on the fact that multiplying the length of one of the sides by $\frac13$ or $\frac23$ has the effect of multiplying the area of the triangle by the same number.
This relies on the fact that multiplying the length of one of the sides by $\frac13$ or $\frac23$ has the effect of multiplying the area of the triangle by the same number.This is because, while the base (any of the sides) remains unchanged, the perpendicular height is multiplied by $\frac13$ or $\frac23$.
A very clear method using this idea is shown below:
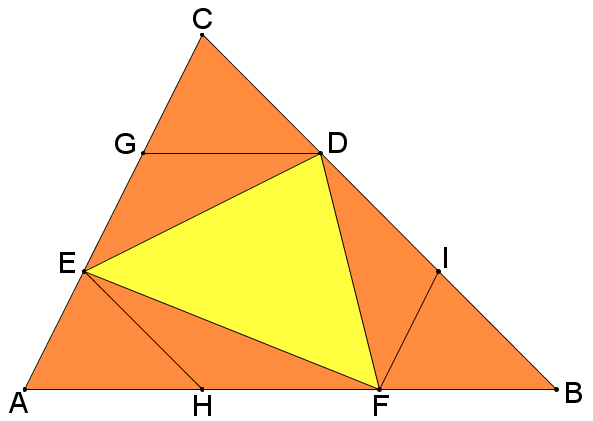
Now, triangle $AHE$ is an enlargement of $ABC$ by scale factor $\tfrac{1}{3}$, as $AE=\tfrac{1}{3}AC$, $AH=\tfrac{1}{3}AB$ and $\angle EAH = \angle CAB$.
This means the area of $EAH$ is $\left( \tfrac{1}{3} \right)^2 = \tfrac{1}{9}$ of the area of $ABC$.
Since $HF = AH$, $EAH$ and $EHF$ have the same base length and the same perpendicular height (that of $E$ above $AB$), they have the same area: $\tfrac {1}{9}$ of the total area of $ABC$.
This process can be repeated at vertices $B$ and $C$, so each of the six orange triangles all have area $\tfrac{1}{9}$ of that of $ABC$.
Therefore the yellow area is $1-6\times \tfrac{1}{9} = \tfrac{1}{3}$ of the area of the whole triangle.