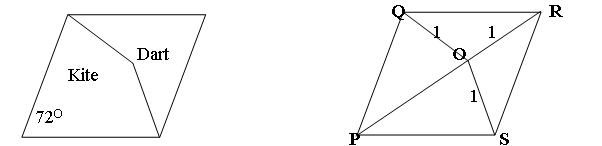
The diagram shows a rhombus $PQRS$ with an internal point $O$ such that $OQ = OR = OS = 1$ unit. Penrose used this rhombus, split into two quadrilaterals, a dart and a kite, to make his famous tiling which fills the plane but, unlike a tessellation, does not repeat itself by translation or rotation.

Find all the angles in the diagram, show that $POR$ is a straight line and show that triangles $PRS$ and $QRO$ are similar. Hence prove that the length of the side of the rhombus is equal to the Golden Ratio $(1+ \sqrt{5})/2$.