 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Look Before You Leap



- Problem
- Getting Started
- Student Solutions
Well done all of you who sent in good solutions to this problem! Many different methods were used. Saul Foresta and Julia Collins found and used the exact value of $\tan 22.5$ degrees which they found using trig formulae; Andre Lazanu used similar triangles; Kamen Marinov used the Sine Rule and Pythagoras Theorem; Hyeyoun Chung, Arun Ayer, Ngoc Tran and Yatir Halevi used the angle bisector theorem ($BA$:$AO$=$BN$:$NO$); Robert Goudie used an ingenious construction; and Dorothy Winn used several applications of the Sine Rule.
Robert Goudie's solution.
If you take triangle $AON$ and double its size you form triangle $ACR$ since $AC$ is double $AO$.
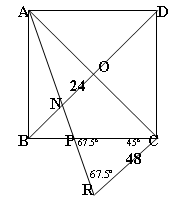
So we now have two similar triangles $AON$ and $ACR$ and it is clearly the case that $CR$ is double $ON$ so $CR = 48$.
Since $AR$ is the bisector of angle $OAB$ we know that angle $CAR = 22.5^{\circ}$ . Therefore angle $CRA = 67.5^{\circ}$.
Angle $RCP$ must be $45^{\circ}$since angle $ACB$ is $45^{\circ}$ and angle $ACR$ is $90^{\circ}$. This implies that angle $CPR$ is $67.5^{\circ}$ since $180 - 45 - 67.5 = 67.5$.
Therefore triangle $PCR$ is isosceles and so $PC = CR$ and hence $PC = 48$ units.
Andre Lazanu's solution using similar triangles
I know that in a square the diagonals are also bisectors (in fact, this is true for the rhombus, and the square is a particular case of rhombus), so angle $BAC$ and angle $DAC$ have both the same measure: $45^{\circ}$. The angles formed by the bisector of angle $BAC$ with the sides of the angle have the following measure: $22^{\circ}30`$.
I noted with $L$ the side of the square, using the Pythagorean Theorem, $AC = L\sqrt{2}$
Now, I observe that $AO$ is half $AC$: $AO = (L\sqrt{2})/2$
Triangles $AON$ and $ABP$ are similar, because each one has a right angle, and there is another pair of equal angles (the ones formed by the bisector). So, I have:
$$\frac{AO}{AB} = \frac{AN}{AP} = \frac{ON}{BP}$$
So, I obtain the following proportion:
$(L\sqrt{2}/2) / L = 24/BP$
$BP = 48 / \sqrt{2} = 24\sqrt{2}$ (units)
Now, I see that angle $BPA$ has $67^{\circ}30`$ and angle $BNP$ has the same measure, so triangle $BNP$ is isosceles with $BP = BN$.
Here I observe that triangles $ABN$ and $ACP$ are similar, because their angles are respectively equal. So
$$\frac{AB}{AC} = \frac{BN}{PC} = \frac{AN}{AP}$$
As $AB / AC = 1 / \sqrt{2}$ it follows that $PC = \sqrt{2}BN$.
So
$PC = \sqrt{2}BN = \sqrt{2}BP = 48$.