Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Square World
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
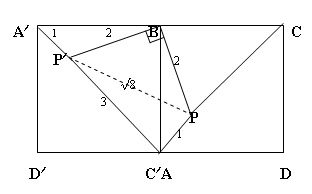
This beautifully neat solution was sent in by Johnny Chen.
If we rotate the figure by $90$ degrees about $B$ (clockwise).
This should result in a new square $A'BC'D'$ with a point $P'$
inside the new square such that, $\angle PBP'=90^{\circ}$ and
$BP=BP'=2$. By Pythagoras, $PP'= \sqrt 8$. Now consider triangle
$AP'P$. The side lengths are $3$, $\sqrt 8$, and $1$ which
satisfies Pythagoras again: $3^2 - 1^2 = (\sqrt 8)^2$.
So this triangle has $90$ degrees at $\angle P'PA$. Since we
know that $\angle BPP'=45^{\circ}$ therefore $\angle BPA$ is $135$
degrees.
This alternative method comes from Yatir from Maccabim-Reut High School, Israel.
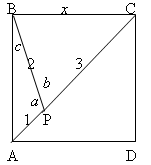
$AB=BC=CD=AD=x$, $BP=2$, $CP=3$, $AP=1$. Name the angles this way: $\angle ABP = c$, $\angle CBP = 90-c$, $\angle APB = a$, $\angle CPB = b$.
We need to find angle $a$. By the Sine Law:
$${x \over \sin b} = {3 \over \sin(90-c)} = {3\over \cos c}$$
and
$${x\over \sin a} = {1 \over \sin c}$$
Hence $\sin c = \sin a /x$, $\cos c = 3\sin b /x$ and we use the identity $\sin ^2 c + \cos ^2 c = 1$ to eliminate $c$. So
$$\eqalign { \sin ^2 (a/x^2) + 9\sin ^2 (b / x^2) &= 1 \cr \sin ^2 b &= (x^2 - \sin^2 a)/9.}$$
Using the Cosine Law we find $\cos b$ and then eliminate $b$: $$x^2 = 9 + 4 - 12 \cos b$$ so $$\cos^2 b = [(13-x^2)/12]^2.$$
Using the identity $\sin^2 b + \cos^2 b = 1$ we get $$(x^2 - \sin ^2 a)/9 + [(13 - x^2)^2]/144 = 1 \quad (1).$$
Finally we eliminate $x$. By the Cosine Law $x^2 = 4 + 1 - 4\cos a$ so
$$x^2 = 5 - 4 \cos a \quad (2).$$
Combine (1) and (2) and simplify and we get: $$2 \cos^2 a /9 + 8 /9 = 1$$ hence $\cos^2 a = 1/2.$
This yields solutions: $a=45$ or $a=135$ degrees.
Now this angle cannot be $45$ degrees because angle $c$ is smaller ($AP$ is the shortest side of triangle $APB$) and the third angle of the triangle is less than $90$ degrees. Hence angle $a$ is $135$ degrees.