 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Worms



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thank you to everyone who sent in their solutions for Worms.
Poppy from Dussindale Primary School sent in this excellent solution and took it further with her investigation into number patterns:
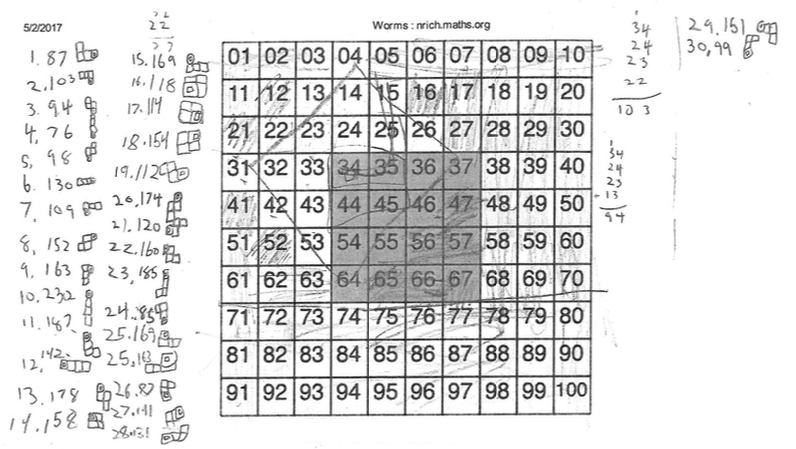
I started with the head of the worm on the number 34.
First of all I began by trying out the different shapes. I rotated each shape through north, east, south and west. I then realised that some of the shapes had a reflection. I started with the L shape and noticed whilst some of the numbers were different that there were repeated totals. I began to investigate why this happened - see the algebra for each of the L
shaped totals. I then looked at the S shaped worm and saw that the reflections came up with repeated totals. I found that there 16 different totals but 24 different calculations that could be made by rotating or reflecting the worms.

From Springvale School we had a number of solutions sent in.
Hannah, working with snakes instead of worms!
I worked out that to get the smallest number for each one, you have to point the snake directly up, and if you want to get the highest possible number for each one you needed to point the snake directly down. I also worked out that there are 32 different positions for each square, that's 512 in total! I know this, because there are different ways the worm can
be positioned and you can put each one, North, East, South, West.
Meg
I worked out to get the smallest possible solution, you need to put the worms head on 34 (the smallest number on the shaded grid) and its body above it so it sits on 34,24,14 and 4 which equals = 76. To get the biggest solution you need to put the worms head on 67 and the body below it on 67,77,87 and 97 this = 328. I worked out that there are 32 solutions for each box. I
found this out because there are 8 different ways that the worm can be positioned and you can make 4 worms, so 4x8=32.
Martha
I worked out that there are 512 solutions for worms....
I know this because there are 8 different ways that each worm can be positioned and there are 4 different worms, and 8 x 4 is 32. Then you must times 32 by 16 as there are 16 places that the worm head could start at, so there are 512 solutions. I also worked out the smallest and the largest possible combination that the worm could possibly lie on here is what I worked
out...
For the smallest the head must start on 34 and go strait up so it would go 34, 24, 14 and then 4 so the total would be 76. For the largest combination you would have to start on 67 and go straight down so it would go , 67, 77, 87 and then 97 so the total would be: 328
Nathan
I know the total amount of solutions is 512 because there are 32 different shapes the worm can make because normally it can make three shapes in every direction so you would get twelve and then you can reverse it all apart from the straight lines because they will just be the same so you get 20. Then you add on the shapes which are squares to get 24 then you have to twist
it up and you get 4 more and then you reverse it to get 32. Finally you need to times 32 by 16 to get 512
Oliver
The way to figure out all the solutions, is to find out how many there are facing one way, to get 4, then times by 2, because you can reverse each shape to get 8. You can also move it around so it is facing different directions so you times it by 4, because it can face 4 different directions, which is 32 solutions then times by 16, which is 512.
Ryan J. & Ryan W. from Imlay Elementary School in the USA sent in this explanation and their workings:
We know that there are 30 possible directions the 4 block worm can go while still being connected properly, while still eating its favorite food in the garden. We also wrote down the sum of the 4 number squares the worm was on, and drew the position so we could check to see if a position was repeated later. The worm head placement we chose was square number 34. The way
we know we found all the worm positions is because we listed the possibilities that the worm can move each time we found a new one.
We also know we found all of them is because we would come up of new positions, and write them down four times, one pointing up, one pointing left, one down, and one right. After we did thirty, we could come up with nothing else.
The way we knew we didn't miss one, is we crossed out all squares that where to far away than 4 blocks from the worm head. Then we made every combination in the area of the non-crossed out squares.
Thank you all for the solutions sent in.