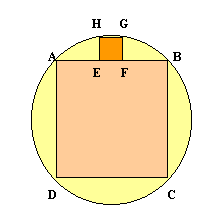
The largest square which fits into a circle is $ABCD$ and $EFGH$ is a square with $E$ and $F$ on the line $AB$ and $G$ and $H$ on the circumference of the circle. Show that $AB = 5EF$.

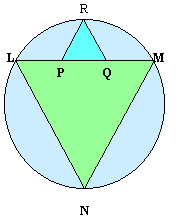
Similarly the largest equilateral triangle which fits into a circle is $LMN$ and $PQR$ is an equilateral triangle with $P$ and $Q$ on the line $LM$ and $R$ on the circumference of the circle. Show that $LM = 3PQ$.