Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Golden Triangle
Age 16 to 18
Challenge Level 





- Problem
- Student Solutions
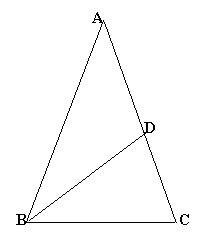
The three triangles $ABC$, $CBD$ and $ABD$ are all isosceles. Find the angles in the triangles.
The sides $AB$ and $BC$ have lengths $p$ and $q$ respectively. Prove that the ratio $p/q$ is equal to the golden ratio $\frac{1}{2} (\sqrt{5}\ +1) $.
and find the ratio $q/p$.The area of triangle $ABC$ is 2 square units. Find the areas of $CBD$ and $ABD$ exactly (i.e. find the areas in the form \[ a + b \sqrt{5} \]
where $a$ and $b$ are rational numbers)