 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Three Cubes



- Problem
- Student Solutions
- Teachers' Resources
Thank you Andrew Clark for this solution.
1. The distances between the centres of two adjacent faces of another cube is $8$cms. What is the side length of this cube?
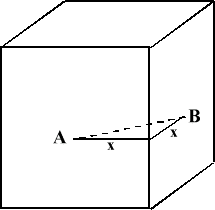
Let the side length of the cube be $ 2x $. From the centre points A and B of both faces to the line at which their planes meet is $ x $, and AB ($ = 8 $) is the hypotenuse of a right angled triangle whose other two sides have length $ x $ . Therefore $ 2x^2 = 8^2 $ , so that $ x= \sqrt{32} $ , and the length of the side is $ 8\sqrt{2} $ .
2. It is known that the area of the largest equilateral triangular section of a cube is $140$cm$^2$ . What is the side length of the cube?
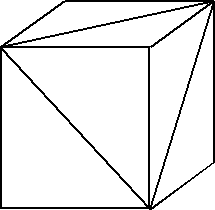
Cube with equilateral triangle section.
Let the sides of the equilateral triangle have length $ a $; then the area of the triangle is $ (a/2)(a\sqrt{3}/2) = a^2\sqrt{3}/4 $. As the area of the triangle is $ 140 {\rm cm}^2 $, $ a^2 = 560/\sqrt{3} $. The length of the diagonal of a face of the cube is $ a $; let $ b $ be the length of a side of the cube. Then, by Pythagoras' Theorem, $ 2b^2 = 560/\sqrt{3} $ so that $ b=12.7 $ to three
significant figures.
3. Another cube has an edge length of $12$cms. At each vertex a tetrahedron with three mutually perpendicular edges of length $4$cms is sliced away. What is the surface area and volume of the remaining solid?
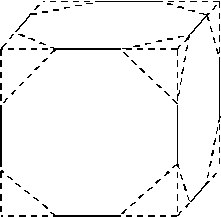
From each face of the cube we remove four triangles whose total area is $ 32 {\rm cm}^2 $ . Thus the area left is $ 144-32 = 112 {\rm cm}^2 $ . There are six such faces giving an area of $ 672 {\rm cm}^2 $ . \par In addition, there are eight equilateral triangular faces of side length $ 4\sqrt{2} $ . The total area of these is $ 8 \times 8\sqrt{3} = 64\sqrt{3} {\rm cm}^2 $ . Thus the total surface area is $ 672 + 64\sqrt{3} = 783 {\rm cm}^2 $ to the nearest square centimetre.
The volume of a tetrahedron is $ (1/3) \times \hbox{(area of base)} \times \hbox{height} $ . Consider one of the tetrahedra, and take one of the right-angled triangles as its base; then its volume is $ (1/3) \times 8 \times 4 = 32/3 $ . Thus the volume of the remaining solid is $ 12^3 - (8\times 32)/3 = 1643 {\rm cm}^3 $ to the nearest cubic centimetre.