Copyright © University of Cambridge. All rights reserved.
'Plants' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This activity is a good one to choose when wanting to encourage children to think creatively and 'have a go' at problem solving. It is also accessible to a wide range of attainment levels. This activity can also be a platform from which to give opportunities for children to talk freely about their thinking and to
encourage them really to listen to each other.
Possible approach
Before you embark upon this activity with pupils, I do suggest that you play around with it a bit on your own or with colleagues. This is often a good idea, but in this case I think it is particularly valuable as you find that interesting strategies come into play that you probably would not have thought about had you not indulged yourself.
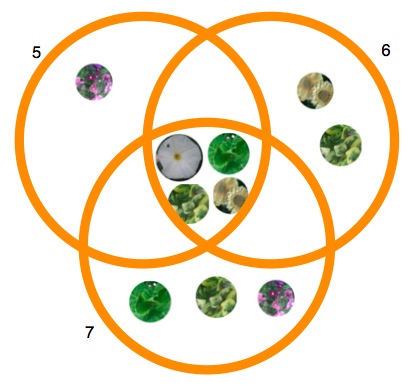
You could, with some youngsters, just introduce three hoops and a number of counters (to represent plants) and, having labelled the hoops with the quantities that need to be inside, ask the youngsters to see if they can find a solution. With the suggested $5$, $6$ and $7$ for each of the three circles, you could explore the activity using between $7$ and $18$ counters. It would be quite
something for some of your pupils to explore all the different possibilities with each of the numbers from $7$ through to $18$, particularly with the emphasis on talking, listening and discussion.
Key questions
How many are there now in this part?
How could we make this part have a correct number in it?
Possible extension
a. This idea actually came from a pupil doing this investigation. She labelled each area and then produced a table to show the number of plants in each.
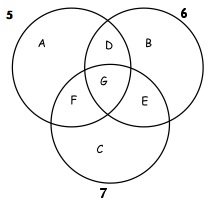
Pupils might consider the areas D, E, F and G as "worth" more than $1$, (D, E, F being $2$ and G $3$) and record results in a table. There's a lot to explore in such tables, and it's interesting at the start to find out how the pupils explore to get the table. Some may be using a spreadsheet, or mental calculations, or just looking at the picture of
three overlapping circles, whilst others may use something practical to check that all is well with their ideas. Some interesting discussions may arise from some pupils who work very arithmetically and come up with a system but unfortunately ignore the maximum number allowed in each circle.
b. Explore other groups of numbers instead of just $5$, $6$ and $7$ - what about numbers going up in $2$s, $4$s, $6$s and $8$s or any other number?
c. If pupils have happily constructed tables in which every possibility is discovered, you might explore the number of possibilities according to the difference between the total for the three circles if they were no overlaps, ($5+6+7=18$) and the number of items used. For example there were seven solutions for a difference of two:
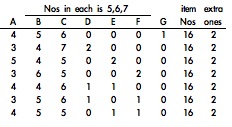
Further exploration will reveal the number of solutions when $3$, $4$, $5$ etc. extra ones are needed (e.g. when $13$ items are used with $5$, $6$ and $7$ circles then there an extra ($18 - 13$) five items needed.
For more extension work
Obvious extension work can be looked at by considering four or more areas - so take yourselves to More Children and Plants.
Possible support
I feel that the best support is to be alongside the children being the 'more mature thinker' in that you can more easily help them to keep track of where they are and prompt them to suggest the next move.