Ben has solved this Tough Nut. He did not say which school he comes from.

The probability of winning a 15 frame match was shown in the problem Snooker to be $0.2131$ for a weaker player who has a consistent probability of $0.4$ of winning each single frame. We use the same method here.

To win an 11 frame match the player must be the first one to win 6 frames. He may win 6 games outright or win any 5 of the first 6 games and lose one then win one, or any 5 of the first 7 games and lose 2 then win one, or any 5 of the first 8 games and lose 3 then wins one or any 5 of the first 9 games and lose 4 then win one or any 5 of the first 10 games and lose 5 then win one. The probability is $$p^6 + {6\choose 5}p^5(1-p)p + {7 \choose 5}p^5(1-p)^2p + {8 \choose 5}p^5(1-p)^3p+{9\choose 5}p^5(1-p)^4p+ {10 \choose 5}p^5(1-p)^5$$ For $p=0.4$ and $1-p=0.6$ this becomes $$0.4^6[1 + 6 \times 0.6 + 21 \times 0.6^2 + 56 \times 0.6^3 + 126 \times 0.6^4 + 252 \times 0.6^5 = 0.2465018$$ As $0.2465 > 0.2131$ this result gives evidence that weaker players are more likely to win 11 frame matches than they are to win 15 frame matches.



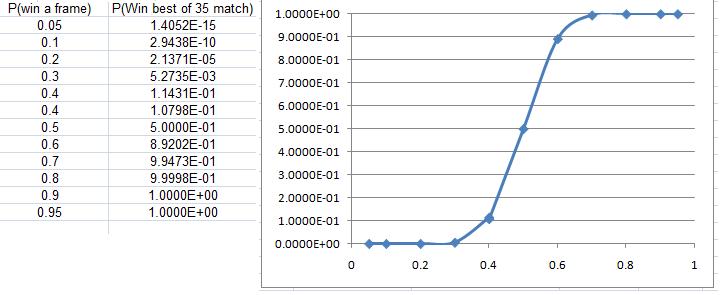
James from Bay House school did a numerical investigation and showed that the chances of winning the tournament were very slight with a 0.4 chance of winning each frame.

Even with a 40% chance of winning each frame, the chance of being the first to 18 frames is less than 1 in 10 million!


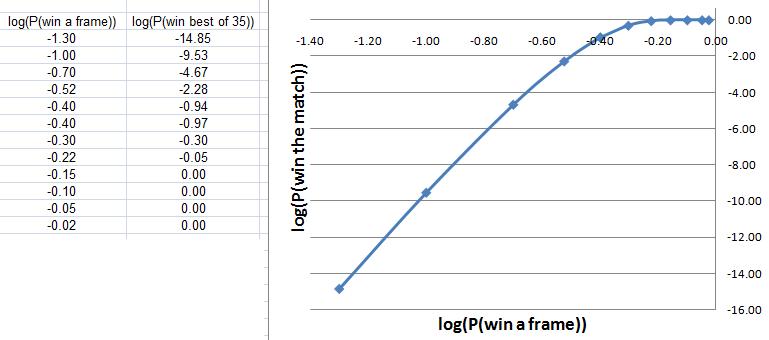
We can also look at the chance of being the first to 18 frames for different probabilities of winning each frame.

If you plot a log-log graph then you can see a highly linear relationship for values of probability less than about $90$ percent.