Six Discs
Problem
Six circular discs, all of radius 1 unit, are packed in different-shaped boxes so that the discs touch their neighbours and the sides of the box.
- Without using any calculations, compare the areas of the bases of boxes A and B and say which is the larger.
- Use estimation to list the packings in order of increasing base area. Which are the hardest to put in order?
- Now calculate the area of the base of each box and compare the correct order with your estimate.
Image
|
||
Getting Started
What would happen if you superimposed B on A? What about D on E?
These diagrams show some right-angled triangles you can use to work out the lengths on shapes B and D using trigonometry. What angles do you know? What sides do you know?
Student Solutions
Hee Chan and Jeang Bin sent us their working with correct areas for shapes A and C:
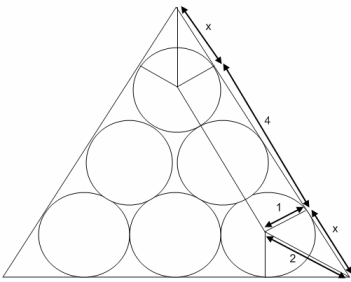
The longer part of the rectangle is $4$ because each circle has radius $1$ unit.
The right-angled triangle with side length marked $x$ has angles $30^{\circ}, 60^{\circ}$ and $90^{\circ}$ so its hypotenuse must be $2$, and side $x$ is $\sqrt{3}$ according to Pythagoras's law.
So the total length of one side of the triangle is $4+2\sqrt{3}$.
The area of the equilateral triangle is
$$\frac{1}{2}(4+2\sqrt{3})^2 \times \sin 60^{\circ}$$ $$=\frac{1}{2}(4+2\sqrt{3})^2 \times\frac{\sqrt{3}}{2}$$ $$=7\sqrt{3}+12$$which is $24.12$ square units to two decimal places.
For C, for the bottom there are 3 circles and this means that the length of the bottom is 6 units. Also for the height there are 2 circles so the length is 4 units. The area is $4 \times 6 = 24$ square units.
In a similar problem Nicola Spittal, S4, Madras College, St Andrew's sent in this excellent solution, demonstrating that A must have a larger than B and also calculating the correct areas for shapes A, B and C.
By superimposing the triangular packing (A) on the parallelogram packing (B) as shown below we can see that $area(\Delta QRS) = area(\Delta STU)$ so that (A) has larger area than (B) and the difference in areas is equal to the area of the small triangle $\Delta UVW$.
We use many 30-60-90 triangles with sides in the ratio $1:2:\sqrt {3}$. The areas of the packings are as follows.
Packing (A)
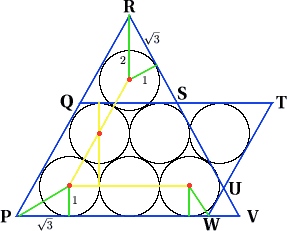
The triangle has side length $4+2\sqrt{3}$ so that area is ${1\over 2}(4+2\sqrt{3})^2 \sin 60^\circ$, or (equivalently, using half base times height) ${1\over 2}(4+2\sqrt{3})(3+2\sqrt{3})$, which is 24.12 square units to 2 decimal places.
Packing (B)
The base length is given by $PW=\tan 60^\circ +4+\tan 30^\circ = \sqrt{3}+ 4 + {1\over \sqrt{3}}= 6.3094.$ The height is given by $h = 2+2\cos 30^\circ = 2 + \sqrt{3}= 3.7321$, so that the area is 23.55 square units to 2 decimal places.
Packing (C)
As the rectangle is $6\times 4$, the area is 24 square units.
Here is one method of finding the area of the remaining shapes:
Packing (D)
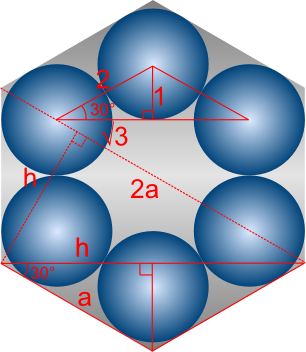
$h = \sqrt{3} + 1$ (from diagram)
$\cos 30^\circ = \frac{h}{a} \Rightarrow a = \frac{h}{\cos 30^\circ} = 2(\frac{\sqrt{3}}{3} + 1)$
Splitting the hexagon in to two trapezia, the area is therefore:
$A_D = 2\{\frac{1}{2}(a + 2a)h\} = \frac{3}{2}ah = \frac{3}{2}(\frac{\sqrt{3}}{3}+1)(\sqrt{3}+1) = 8\sqrt{3}+12 = 25.86 \textrm{ (4 s.f.)}$
Packing (E)
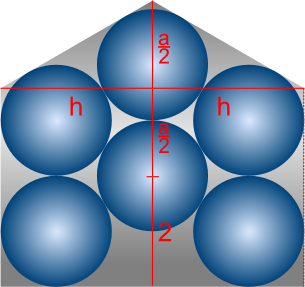
Area composed of triangle, width $2h$ height $\frac{a}{2}$, and rectangle, width $2h$ height $2+\frac{a}{2}$
$\therefore \ A_E = \frac{1}{2}(2h)(\frac{a}{2}) + (2h)(2+\frac{a}{2}) = \frac{3}{2}ah + 4h = 8\sqrt{3} + 10 = 23.86 \textrm{ (4 s.f.)}$
Packing (F)
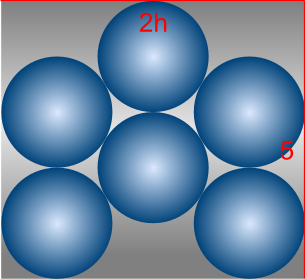
$A_F = 5(2h) = 10h = 10(\sqrt{3}+1) = 27.32 \textrm{ (4 s.f.)}$