Copyright © University of Cambridge. All rights reserved.
'Tiles on a Patio' printed from https://nrich.maths.org/
Show menu
These solutions are just some examples showing the work of four children.
First of all we have Izzy's examples:-
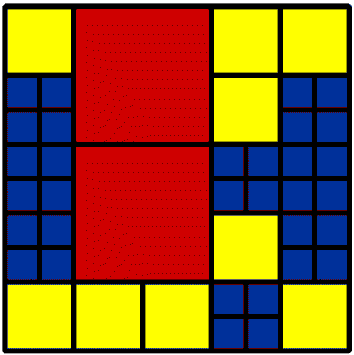 |
9 2 by 2 2 4 by 4 32 1 by 1 43 Total |
 |
96 1 by 1 1 2 by 2 97 Total |
Izzy found that you could not get a solution using 98 or 99 tiles so the next highest after 100 was this one with just 1 2 by 2 replacing 4 1 by 1's.
Now we see Lizzy's:-
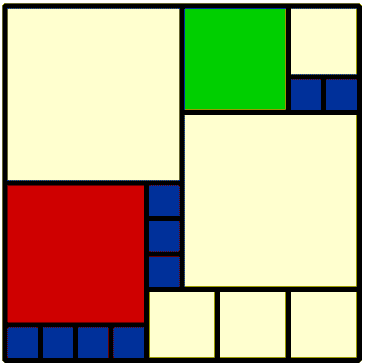 |
2 5 by 5 1 3 by 3 1 4 by 4 4 2 by 2 9 1 by 1 17 Total |
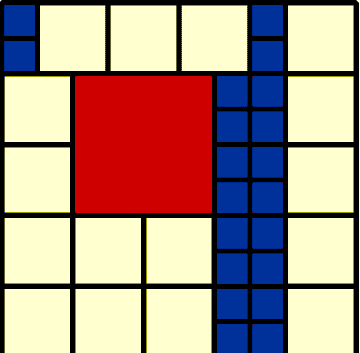 |
16 2 by 2 20 1 by 1 1 4 by 4 37 Total |
I rather liked her 17 made up of 5 different sizes. The 37 was not symmetrical, many results were, that's neither good nor bad ... it's all O.K.
Then we have Ben:-
 |
20 2 by 2 20 1 by 1 40 Total |
 |
8 2 by 2 1 6 by 6 32 1 by 1 41 Total |
His 41 would really look good if you wanted it to be very symmetrical. You could probably invent some games in going around the edge from 4 1 by 1's to a 2 by 2. The 40 is interesting because there is the same number of each tile size.
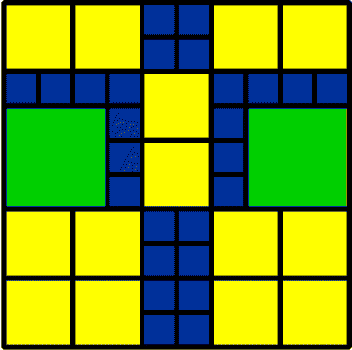 |
14 2 by 2 2 3 by 3 26 1 by 1 42 Total |
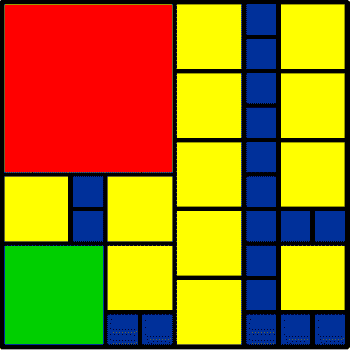 |
12 2 by 2 1 3 by 3 1 5 by 5 18 1 by 1 32 Total |
I think Bo's 42 is rather like a robot! The 32 was very different.
Well done and thank you Izzy, Lizzy, Ben and Bo. Yes these are four real children from the South West of England who were in a group of 19 doing this activity.