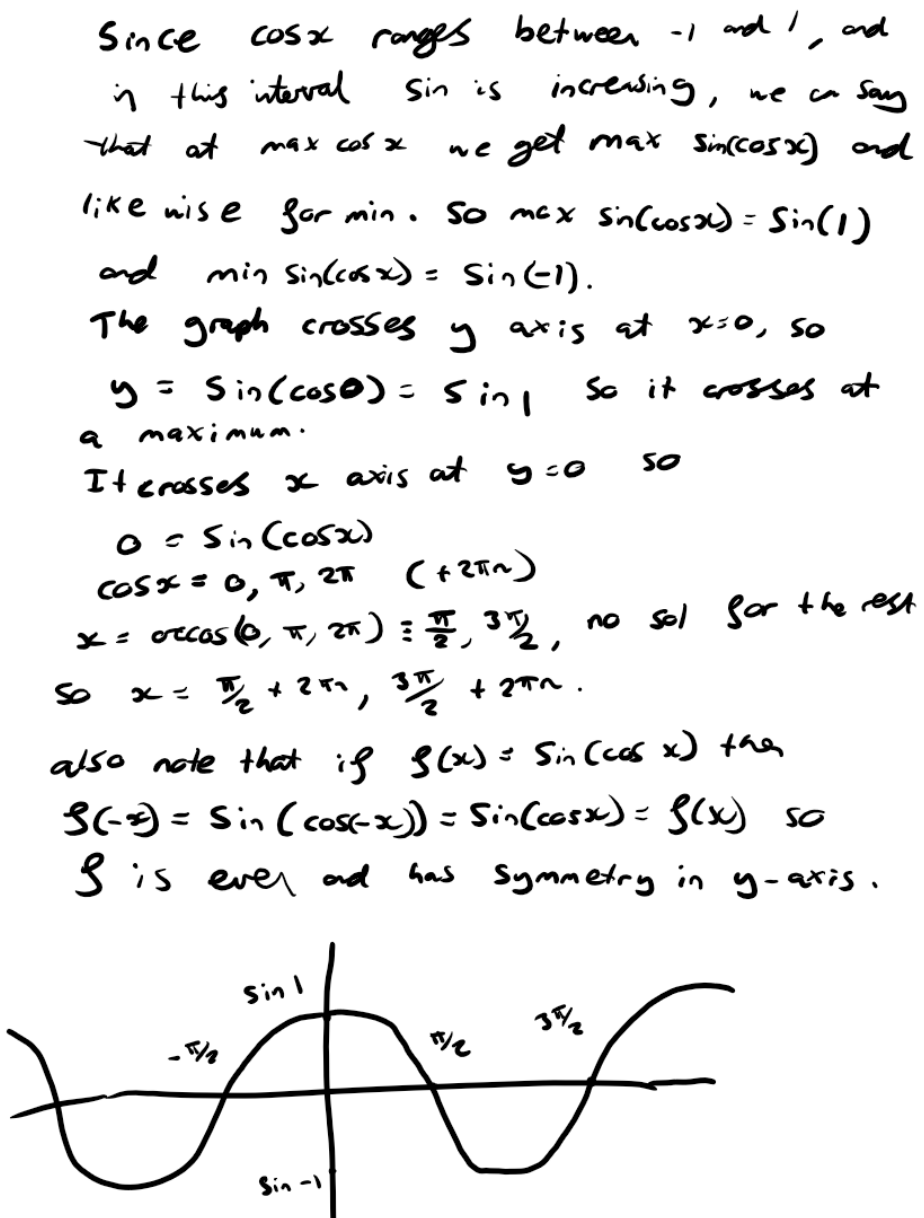Well done to Dylan from Brooke Weston and Joshua from Bohunt Sixth Form in the UK who both sent full solutions.

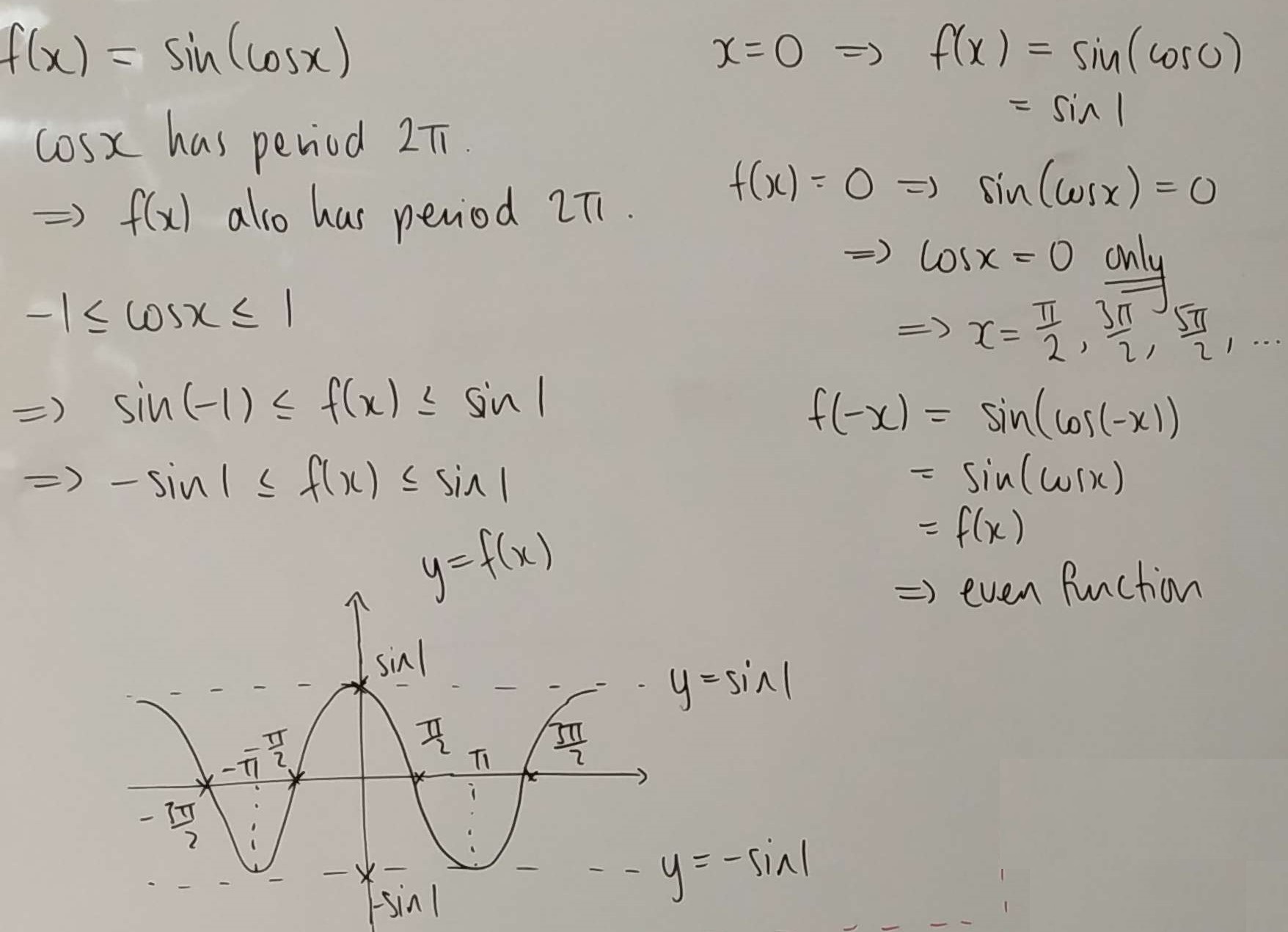
Joshua sketched the graph of $y=\sin{(\cos x)}$ by considering the minimum and maximum values of $\cos x,$ where the function should be increasing and decreasing, and where the function should cross the co-ordinate axes:

Dylan sketched the graph of $y=\sin{(\cos x)}$ by considering the periodicity and symmetry of $\cos x$ as well as the minima, maxima and roots of the function:

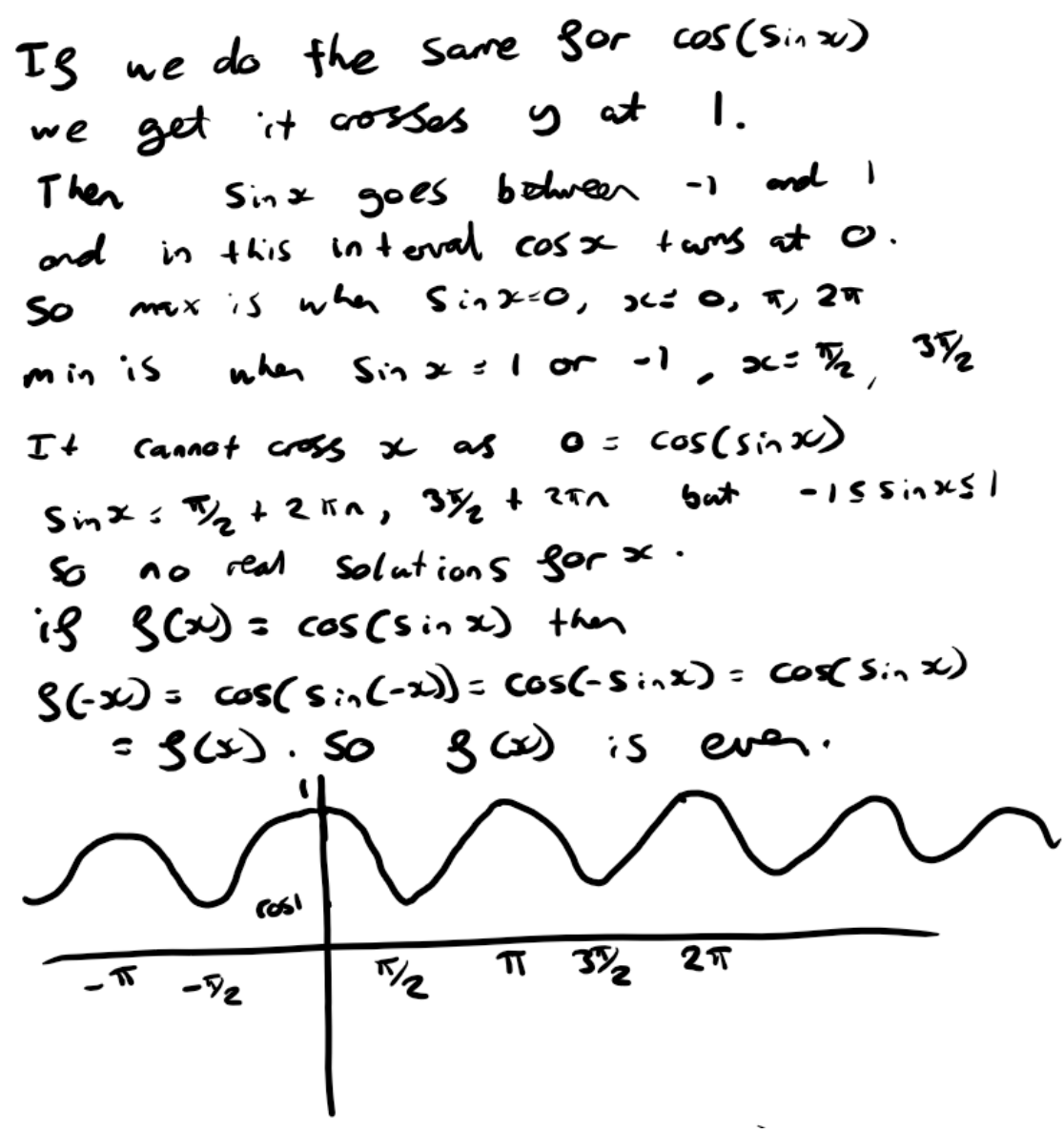
Dylan and Joshua both used the same method they'd used before for the graph of $y=\cos{(\sin x)}.$ This is Joshua's work:

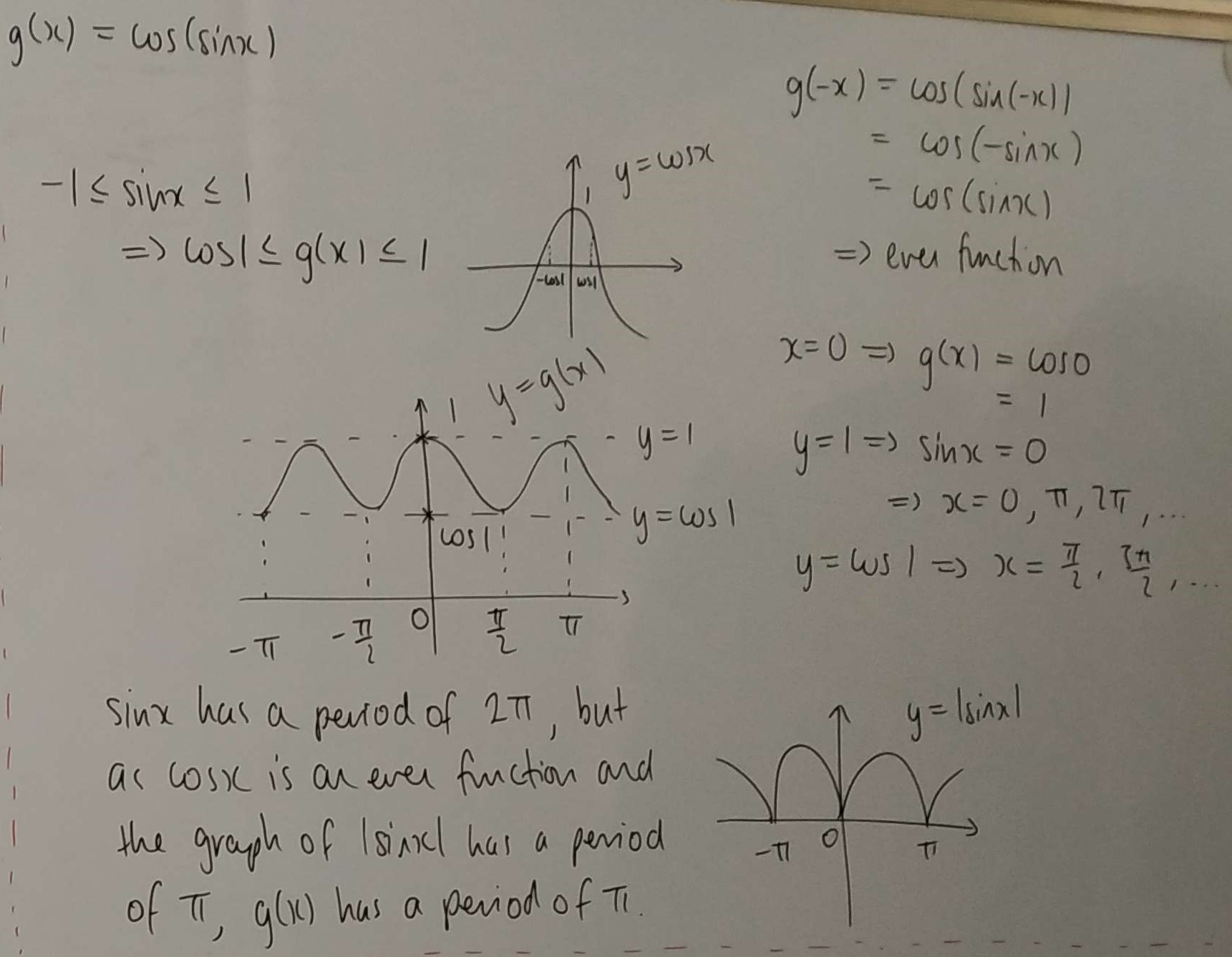
This is Dylan's work:

Dylan and Joshua both completed the rest of the problem - building up to showing that $\cos{(\sin x)}\gt\sin{(\cos x)}$ (or, in Dylan's words, $g(x)\gt f(x)$) for all $x.$ This is Dylan's work: