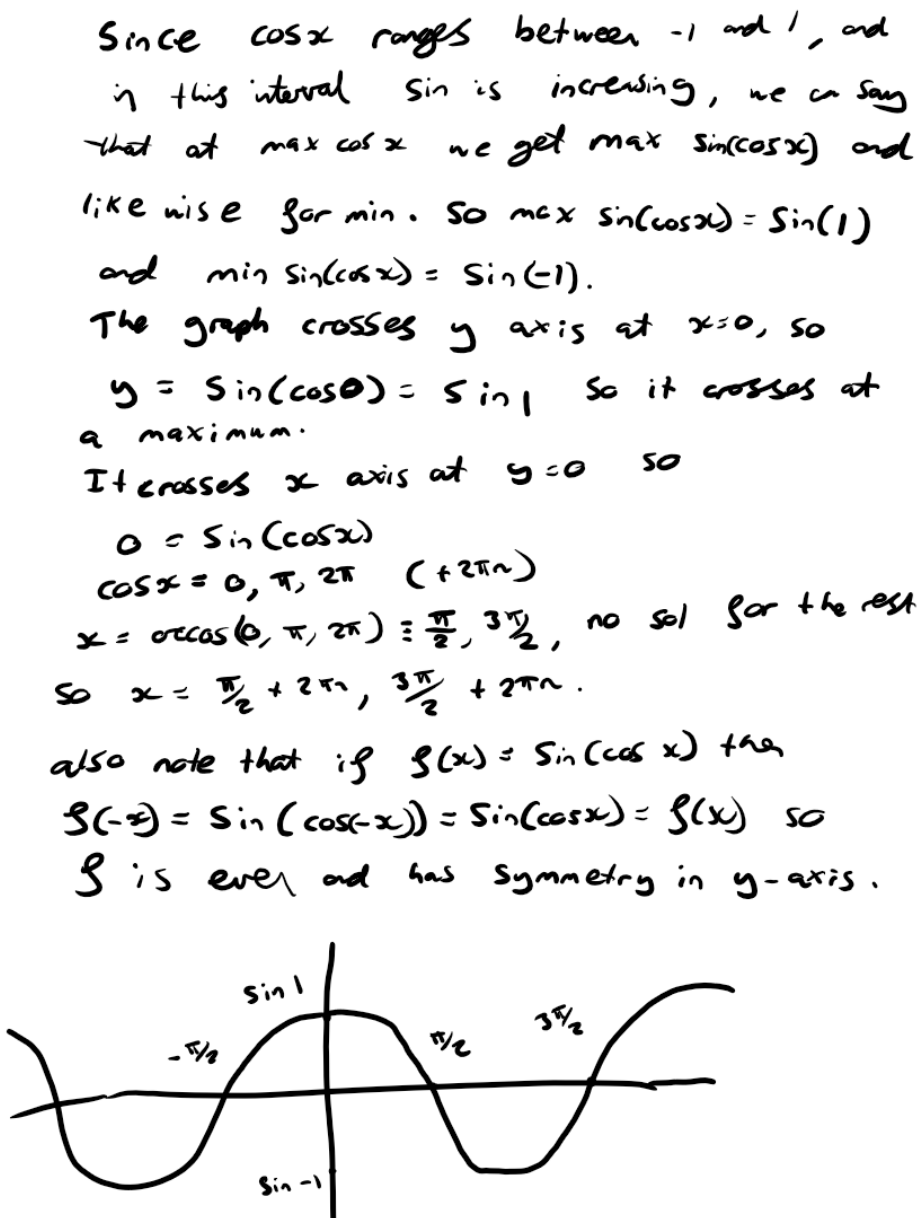Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Making Waves



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to Dylan from Brooke Weston and Joshua from Bohunt Sixth Form in the UK who both sent full solutions.
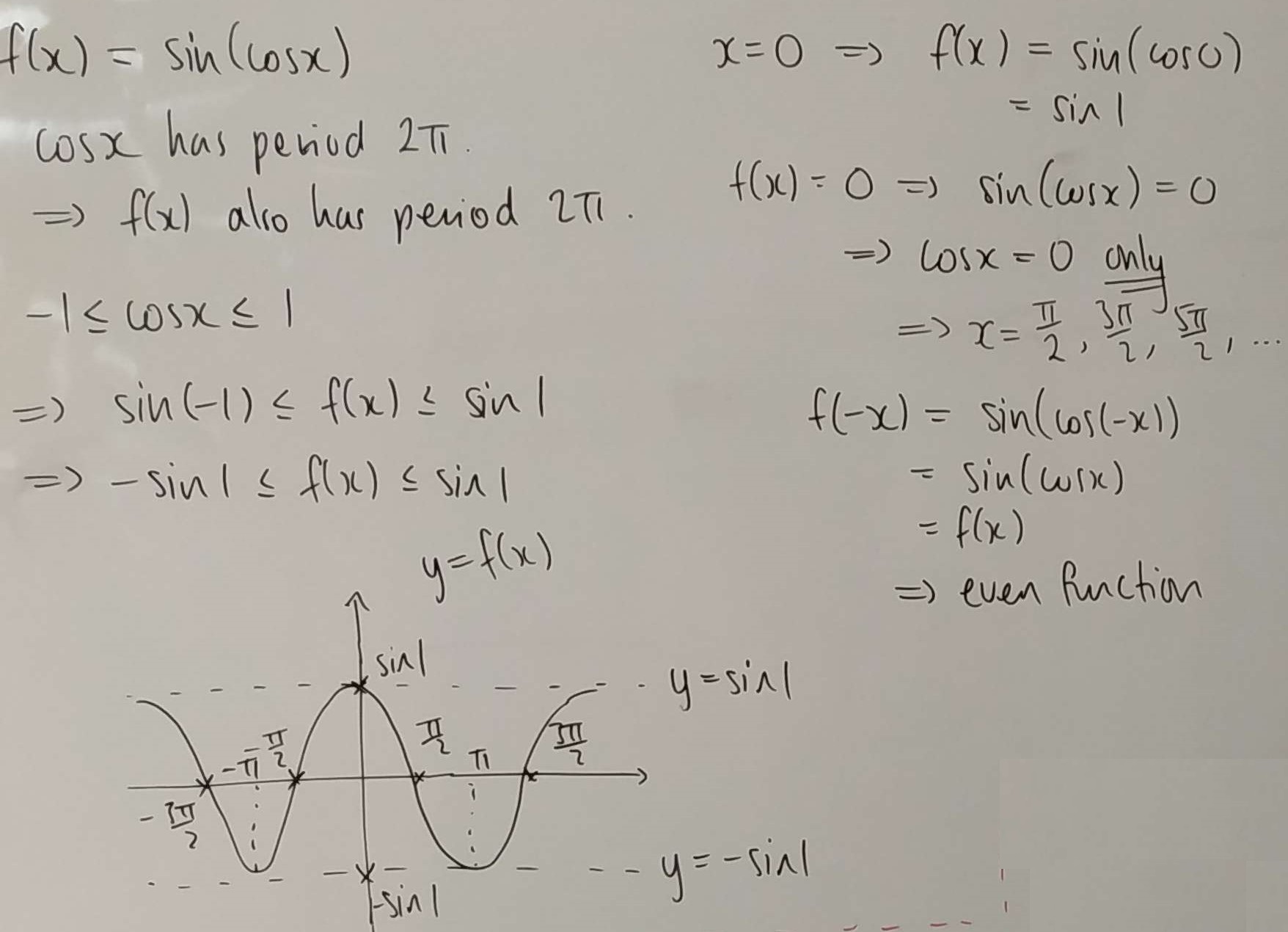
Joshua sketched the graph of $y=\sin{(\cos x)}$ by considering the minimum and maximum values of $\cos x,$ where the function should be increasing and decreasing, and where the function should cross the co-ordinate axes:
Dylan sketched the graph of $y=\sin{(\cos x)}$ by considering the periodicity and symmetry of $\cos x$ as well as the minima, maxima and roots of the function:
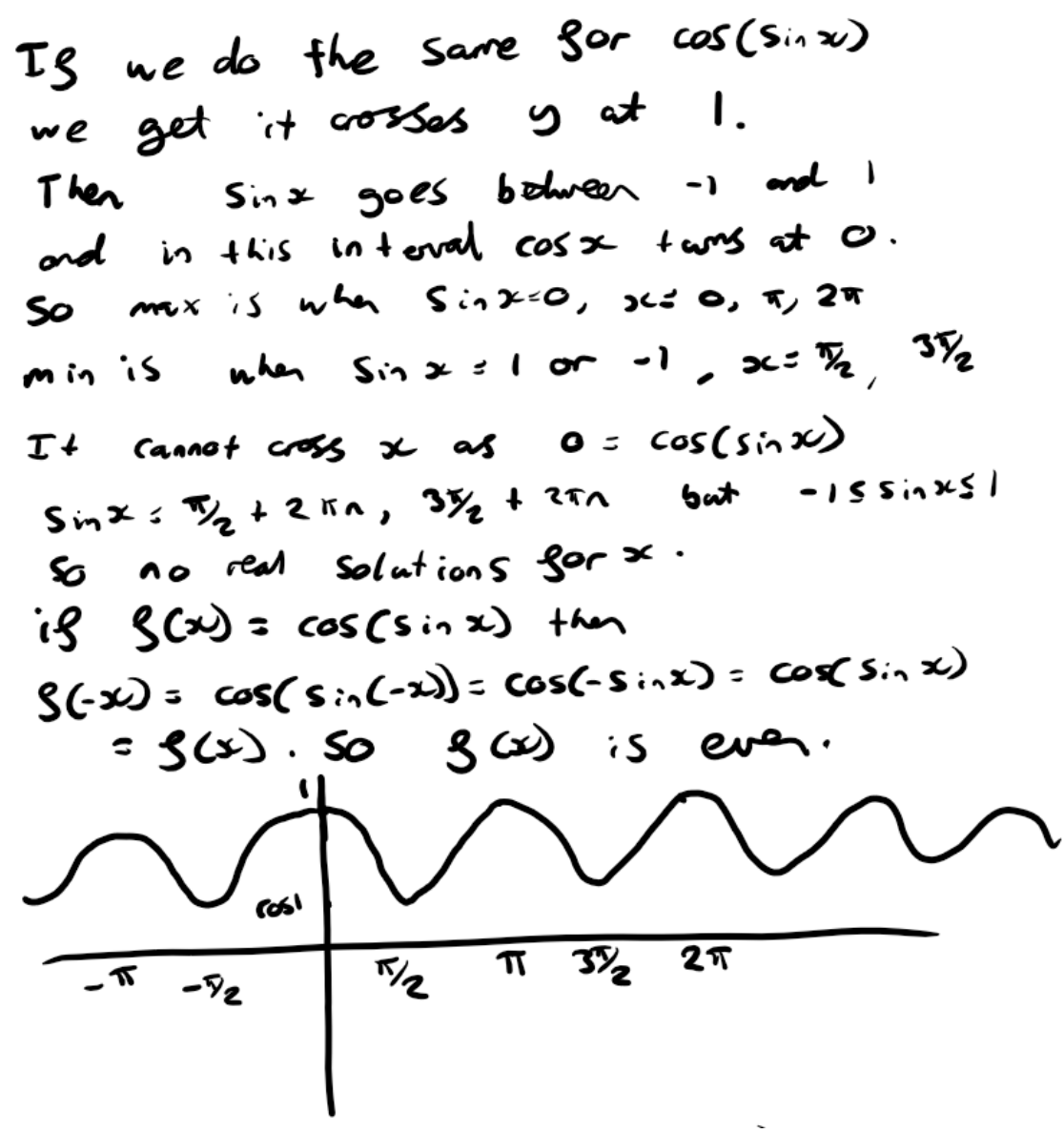
Dylan and Joshua both used the same method they'd used before for the graph of $y=\cos{(\sin x)}.$ This is Joshua's work:
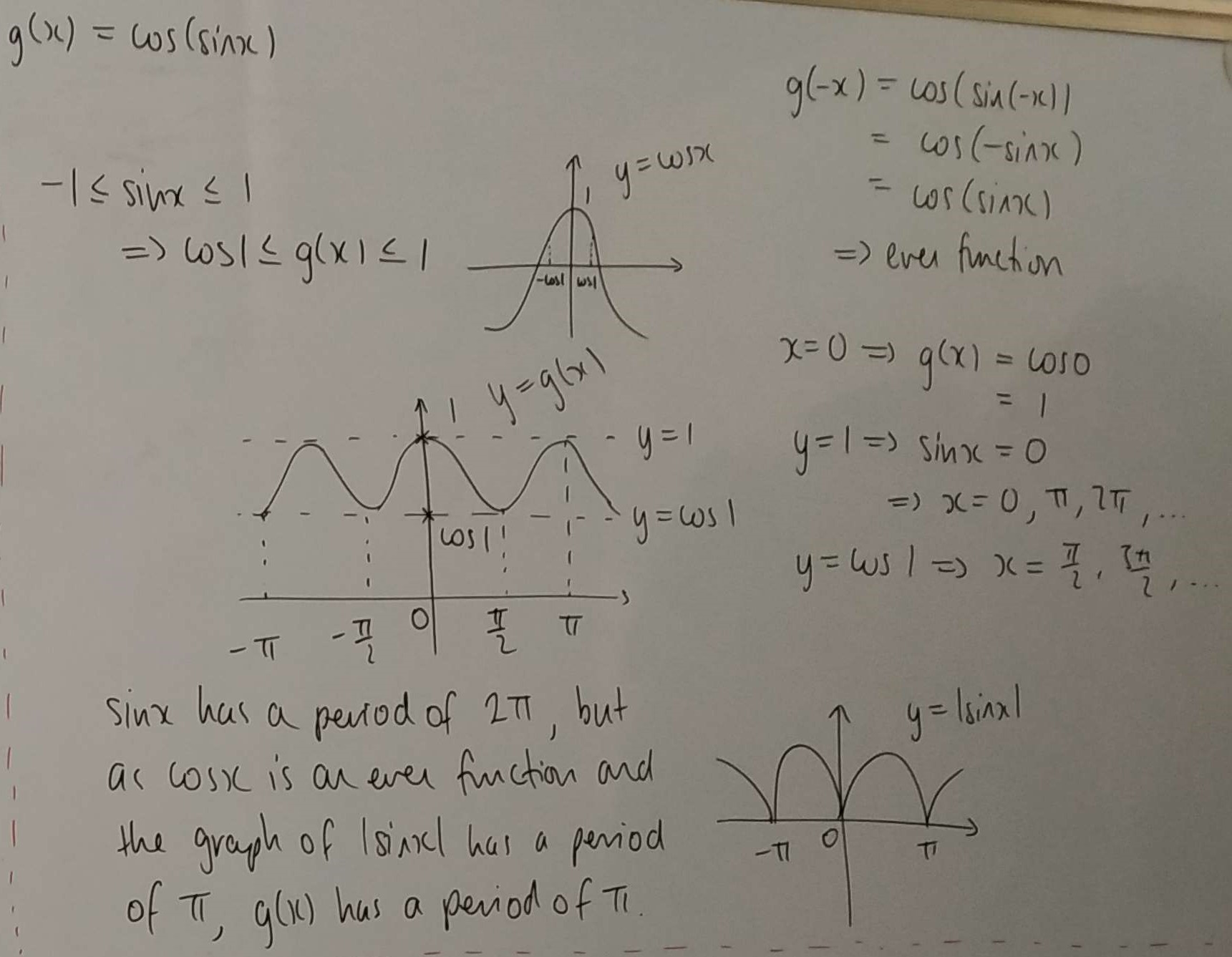
This is Dylan's work:
Dylan and Joshua both completed the rest of the problem - building up to showing that $\cos{(\sin x)}\gt\sin{(\cos x)}$ (or, in Dylan's words, $g(x)\gt f(x)$) for all $x.$ This is Dylan's work: