 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Medallions



- Problem
- Student Solutions
This solution was sent in by Liwei Deng, aged 17, of The Latymer School in London.
First of all, join up the centres of the three circles. This
will form a triangle with side lengths $x+9$, $x+4$ and $13$.
Then draw vertical and horizontal lines as shown to create three
right-angled triangles (shaded on diagram).
Taking the unknown radius to be $x$, we can mark on the lengths
shown in green.
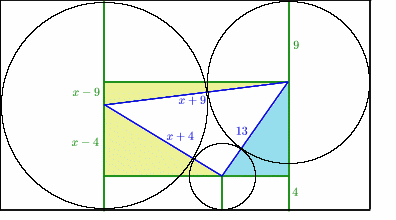
We can now use Pythagoras' Theorem on the two yellow right-angled triangles to find the missing sides. The upper one is $6 \sqrt{x}$,
and the lower one is $ 4 \sqrt{x}$ .
Now we move to the pale blue shaded triangle.
The horizontal side can be found by subtracting:
$$ 6\sqrt{x} - 4\sqrt{x} = 2\sqrt{x}.$$
The vertical side can also be found by subtracting: as we know
that the height of the rectangle is $2x$, this side must be $2x-9-4
= 2x-13$.
Using Pythagoras' Theorem on this triangle, we find that
$$ (2\sqrt{x})^2 + (2x-13)^2 = 13^2 $$ $$ 4x + 4x^2 - 52x + 169 =
169 $$ $$ 4x^2 - 48x = 0 $$ $$ 4x(x - 12) = 0 $$ $$ x = 12 $$.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?