Quartics

Congratulations to Aleksander Twarowski from Gdynia Bilingual High School No 3, Poland for solving this Tough Nut. Well done!


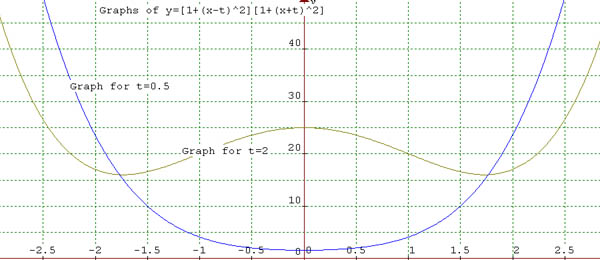
We can observe that for $t=2$ it has 3 stationary points (derivative is equal to 0), 2 minima and 1 maximum. It is an even function symmetrical about the $y$-axis. The function and its graph are the same for $t=-1/2$ as for $t=1/2$.

Let's expand this formula: $$\eqalign{ y&=[1+(x-t)^2][1+(x+t)^2] \cr &= [x^2 + (1+t^2) - 2tx][x^2 +(1+t^2)+2tx]\cr &= x^4 +2x^2(1+t^2)+(1+t^2)^2 - 4t^2x^2\cr &= x^4 +2(1-t^2)x^2 +(1+t^2)^2}$$ When we find its derivative with respect to $x$ we obtain $$y'=4x^3+4x(1-t^2)= 4x[x^2+(1-t)(1+t)]$$ Now we can investigate stationary points when $$4x[x^2+(1-t)(1+t)]=0.$$ It is important to observe that $[x^2+(1-t)(1+t)]$ can be factorized only when $(1-t^2)$ is negative or zero, that is $t^2\geq 1$. So there are three stationary points when $t$ belongs to interval from negative infinity to -1 and from 1 to positive infinity. Hence, we can state that when $t$ belongs to $[-1,1]$ the graph looks like it does for $t=1/2$ above, and when $t$ belongs to $(-\infty,-1)$ or $(1,+\infty)$ the graphs have three stationary points and look like the one for $t=2$ above. Because these three intervals include all real values of $t$, the graphs cannot have other shapes.